题目内容
已知
，
，
，是平面向量，下列命题中真命题的个数是（ ）
①（
•
）•
=
•（
•
）
②|
•
|=|
||
|
③|
+
|2=（
+
）2
④
•
=
•
⇒
=
．
| a |
| b |
| c |
①（
| a |
| b |
| c |
| a |
| b |
| c |
②|
| a |
| b |
| a |
| b |
③|
| a |
| b |
| a |
| b |
④
| a |
| b |
| b |
| c |
| a |
| c |
分析：根据向量数量积的定义与运算性质、向量模的公式，对各项中的等式依次加以分析，可得只有③中的等式是正确的，其它各项都可以举出反例，从而不正确．
解答：解：对于①，由于向量的数量积是一个实数
所以（
•
）•
是与向量
共线的一个向量，
•（
•
）是与向量
共线的一个向量，
而
与
不一定共线，故（
•
）•
≠
•（
•
），得①不正确；
对于②，由向量数量积的定义，可得
•
=|
|•|
|cosθ，其中θ是两个向量的夹角
因此|
•
|=|
|•|
|•|cosθ|≤|
|•|
|，得②不正确；
对于③，根据向量模的公式得|
+
|=
∴|
+
|2=（
+
）2 成立，可得③正确；
对于④，由向量数量积的定义，
可得
•
=
•
即
、
在
上的投影相等，不一定有
=
，故④不正确
因此正确的命题只有③
故选：A
所以（
| a |
| b |
| c |
| c |
| a |
| b |
| c |
| a |
而
| a |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
对于②，由向量数量积的定义，可得
| a |
| b |
| a |
| b |
因此|
| a |
| b |
| a |
| b |
| a |
| b |
对于③，根据向量模的公式得|
| a |
| b |
(
|
∴|
| a |
| b |
| a |
| b |
对于④，由向量数量积的定义，
可得
| a |
| b |
| b |
| c |
| a |
| c |
| b |
| a |
| c |
因此正确的命题只有③
故选：A
点评：本题给出关于向量数量积的几个命题，判断它们的真假性．着重考查了向量数量积的定义与运算性质、向量模的公式等知识，属于中档题．
练习册系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
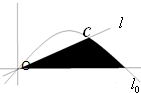已知直线l与抛物线C，当直线l从l0开始在平面上绕O点按逆时针方向匀速旋转（旋转的角度不超过90°）时，它扫过的面积S是时间t的函数，则函数图象大致是（ ）
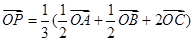，则点 P 一定为三角形的 （ ）
A.45° B.60°