题目内容
直线ax+by=1与圆x2+y2=1相交于不同的A,B两点(其中a,b是实数),且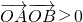 (O是坐标原点),则点P(a,b)与点(0,
(O是坐标原点),则点P(a,b)与点(0, )距离的取值范围为
)距离的取值范围为
- A.(1,+∞)
- B.(
 )
) - C.(
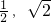 )
) - D.
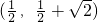
D
分析:设出点A、B的坐标,将直线与圆的方程联立,利用根与系数的关系即可表示出判别式△与 ,即可得出a、b满足的条件,进而利用两点间的距离公式即可得出.
,即可得出a、b满足的条件,进而利用两点间的距离公式即可得出.
解答:当b≠0时,设A(x1,y1),B(x2,y2),联立 ,消去y得到(a2+b2)x2-2ax+1-b2=0,
,消去y得到(a2+b2)x2-2ax+1-b2=0,
∵直线ax+by=1与圆x2+y2=1相交于不同的A,B两点,∴△=4a2-4(a2+b2)(1-b2)>0,化为a2+b2>1.(*)
由根与系数的关系得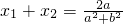 ,
,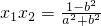 .
.
∵ >0,∴x1x2+y1y2>0,
>0,∴x1x2+y1y2>0,
又ax1+by1=1,ax2+by2=1,
∴b2y1y2=(1-ax1)(1-ax20,
∴(b2+a2)x1x2-a(x1+x2)+1>0,
代入得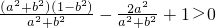 ,化为a2+b2<2.(**)
,化为a2+b2<2.(**)
联立(*)(**)得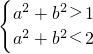 ,当b=0时也成立.
,当b=0时也成立.
画出图象:
当P分别取(0,1),(0,- )时,|QP|取得最小值与最大值,
)时,|QP|取得最小值与最大值,
∴|QP|满足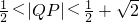 .
.
因此点P(a,b)与点(0, )距离的取值范围为
)距离的取值范围为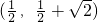 .
.
故选D.
点评:熟练掌握直线与圆相交问题的解题模式、判别式、数量积的计算及两点间的距离公式是解题的关键.
分析:设出点A、B的坐标,将直线与圆的方程联立,利用根与系数的关系即可表示出判别式△与
 ,即可得出a、b满足的条件,进而利用两点间的距离公式即可得出.
,即可得出a、b满足的条件,进而利用两点间的距离公式即可得出.解答:当b≠0时,设A(x1,y1),B(x2,y2),联立
 ,消去y得到(a2+b2)x2-2ax+1-b2=0,
,消去y得到(a2+b2)x2-2ax+1-b2=0,∵直线ax+by=1与圆x2+y2=1相交于不同的A,B两点,∴△=4a2-4(a2+b2)(1-b2)>0,化为a2+b2>1.(*)
由根与系数的关系得
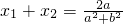 ,
,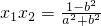 .
.
∵
 >0,∴x1x2+y1y2>0,
>0,∴x1x2+y1y2>0,又ax1+by1=1,ax2+by2=1,
∴b2y1y2=(1-ax1)(1-ax20,
∴(b2+a2)x1x2-a(x1+x2)+1>0,
代入得
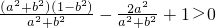 ,化为a2+b2<2.(**)
,化为a2+b2<2.(**)联立(*)(**)得
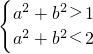 ,当b=0时也成立.
,当b=0时也成立.画出图象:
当P分别取(0,1),(0,-
 )时,|QP|取得最小值与最大值,
)时,|QP|取得最小值与最大值,∴|QP|满足
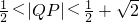 .
.因此点P(a,b)与点(0,
 )距离的取值范围为
)距离的取值范围为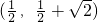 .
.故选D.
点评:熟练掌握直线与圆相交问题的解题模式、判别式、数量积的计算及两点间的距离公式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目