题目内容
如图,直线a、b是异面直线,A、B两点在直线a上,C、D两点在直线b上.求证:BD和AC是异面直线.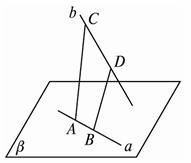
解析:欲证BD和AC是异面直线可用反证法,也可以用判定定理.?
证法一:假设BD和AC不是异面直线,则BD和AC共面,设它们共面于α.?
∵A、B、C、D ∈α,∴AB、CD ![]() α,即a 、b
α,即a 、b ![]() α.?
α.?
这与a、b是异面直线矛盾,故假设不成立.?
∴BD和AC不是异面直线.?
证法二:由条件可知A、B、C三点不在同一直线上,否则a、b为相交直线,与条件矛盾.?
设A、B、C三点确定的平面为α.?
则A、B、C ∈α,于是有D ![]() α,B ∈α,AC
α,B ∈α,AC![]() α,B
α,B ![]() AC.?
AC.?
∴BD和AC不是异面直线.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
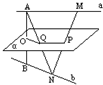
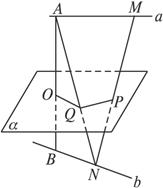
 18、如图,设a、b是异面直线,AB是a、b的公垂线,过AB的中点O作平面α与a、b分别平行,M、N分别是a、b上的任意两点,MN与α交于点P,求证:P是MN的中点.
18、如图,设a、b是异面直线,AB是a、b的公垂线,过AB的中点O作平面α与a、b分别平行,M、N分别是a、b上的任意两点,MN与α交于点P,求证:P是MN的中点.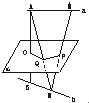 如图,设a、b是异面直线,AB是a、b的公垂线,过AB的中点O作平面α与a、b分别平行,M、N分别是a、b上的任意两点,MN与α交于点P,求证:P是MN的中点.
如图,设a、b是异面直线,AB是a、b的公垂线,过AB的中点O作平面α与a、b分别平行,M、N分别是a、b上的任意两点,MN与α交于点P,求证:P是MN的中点.