题目内容
在 中,已知内角
中,已知内角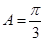 ,边
,边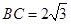 .设内角
.设内角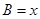 ,
, 的面积为
的面积为 .
.
(1)求函数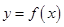 的解析式和定义域;
的解析式和定义域;
(2)求函数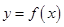 的值域.
的值域.
(1) ,定义域为
,定义域为 ;(2)函数
;(2)函数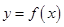 的值域为
的值域为 .
.
解析试题分析:(1)先利用正弦定理将 、
、 用含
用含 的表达式进行表示,然后利用面积公式将函数
的表达式进行表示,然后利用面积公式将函数 求出并进行化简,然后根据对三角形内角的限制求出自变量
求出并进行化简,然后根据对三角形内角的限制求出自变量 的取值范围作为函数
的取值范围作为函数 的定义域;(2)在(1)的基础上,即函数
的定义域;(2)在(1)的基础上,即函数 的前提下,将
的前提下,将 视为一个整体,先求出
视为一个整体,先求出 的取值范围,然后利用正弦函数的图象确定函数
的取值范围,然后利用正弦函数的图象确定函数 的取值范围,即为函数
的取值范围,即为函数 的值域.
的值域.
试题解析:(1)由正弦定理得 ,
, ,
, ,
,

 ,
,
其中 ,即函数
,即函数 的定义域为
的定义域为 ;
;
(2) ,
, ,故
,故 ,
, ,即函数
,即函数 的值域为
的值域为 .
.
考点:1.正弦定理;2.三角形的面积公式;3.二倍角公式;4.辅助角公式;5.三角函数的最值

练习册系列答案
相关题目
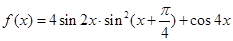 .
. 的最小正周期;
的最小正周期; 在
在 处取得最大值,求
处取得最大值,求 的值;
的值; 的单调递增区间.
的单调递增区间.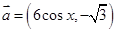 ,
,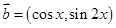 ,
,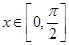 .(1)若
.(1)若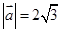 ,求
,求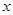 的值;
的值;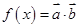 ,求
,求 的最大、最小值.
的最大、最小值.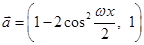 ,
, ,
, ,点A、B为函数
,点A、B为函数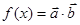 的相邻两个零点,AB=π.
的相邻两个零点,AB=π. 的值;
的值;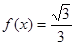 ,
,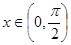 ,求
,求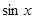 的值;
的值;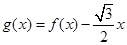 在区间
在区间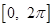 上的单调递减区间.
上的单调递减区间. .
. 时,求
时,求 的最大值和最小值;
的最大值和最小值; 的内角
的内角 所对的边分别为
所对的边分别为 ,且
,且 ,若向量
,若向量 与向量
与向量 共线,求
共线,求 的值.
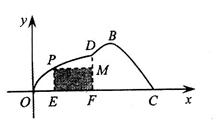
的值. ,另一侧修建一条观光大道,它的前一段
,另一侧修建一条观光大道,它的前一段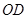 是以
是以 为顶点,
为顶点,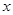 轴为对称轴,开口向右的抛物线的一部分,后一段
轴为对称轴,开口向右的抛物线的一部分,后一段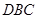 是函数
是函数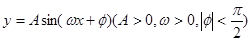 ,
,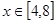 时的图象,图象的最高点为
时的图象,图象的最高点为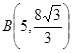 ,
,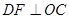 ,垂足为
,垂足为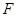 .
.
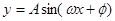 的解析式;
的解析式;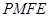 ,问:点
,问:点 落在曲线
落在曲线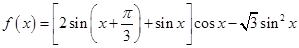 .
. 的图像关于直线
的图像关于直线 对称,求
对称,求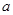 的最小值;
的最小值;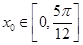 ,使
,使 成立,求实数
成立,求实数 的取值范围.
的取值范围. 为半圆的直径,
为半圆的直径, 为半圆的圆心,
为半圆的圆心, ,
, ,现要将此铁皮剪出一个等腰三角形
,现要将此铁皮剪出一个等腰三角形 ,其底边
,其底边 .
.
 ,求三角形铁皮
,求三角形铁皮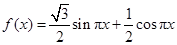 ,
, 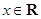 .
. 的最大值和最小值;
的最大值和最小值;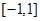 上的图象与
上的图象与 轴的交点从左到右分别为
轴的交点从左到右分别为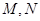 ,图象的最高点为
,图象的最高点为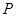 ,
,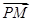 与
与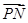 的夹角的余弦.
的夹角的余弦.