题目内容
对于每个正整数n,以s(n)表示满足如下条件的最大正整数:对于每个正整数k≤s(n),n2都可以表示成k个正整数的平方之和.
1.证明:对于每个正整数n≥4,都有s(n)≤n2-14;
2.试找出一个正整数n,使得s(n)=n2-14;
3.证明:存在无限多个正整数n,使得s(n)=n2-14.
解析:用反证法证明如下:
假设对某个n≥4,有s(n)≥n2-14,则存在k=n2-13个正整数a1,a2,…,ak,使得
![]()
于是就有
![]()
从而
![]()
![]() 3b+8c=13
3b+8c=13
这表明c=0或1;但相应的b不为整数,矛盾.
2.每个大于13的正整数m可以表为3b+8c,其中b、c为非负整数.事实上,若m=3s+1,则s≥5,m=3(s-5)+2×8.若m=3s+2,则s≥4,m=3(s-2)+8.

由
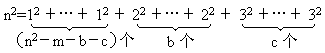
即知n2可表为n2-m个平方和,从而n2可表为n2-14,n2-15,…,
![]()
对于n=13,有
n2=122+52=122+42+32=82+82+52+42
由于82可表为4个42的和,42可表为4个22的和,22可表为4个12的和,所以132=82+82+52+42可表为4,7,10,…,43个平方的和,又由于52=42+32,132可表为5,8,11,…,44个平方的和.
由于122可表为4个62的和,62可表为4个32的和,所以132=122+42+32可表为3,6,9,…,33个平方的和.
![]()
为18+2×9=36,18+2×12=42个平方的和.再由42为4个22的和,132也可表为39个平方的和.
综上所述,132可表为1,2,…,44个平方的和.
![]()
3.令n=2k×13.
因为132可表为1,2,…,155个平方的和,22可表为4个平方的和,所以132×22可表为1,2,…,155×4个平方的和,132×24可表为1,2,…,155×42个平方的和,…,n2=132×22k可表为1,2,…,155×4k个平方的和.
![]()

 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
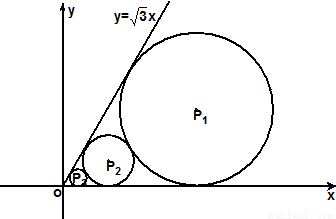
名校提分一卷通系列答案 在xoy平面上有一系列点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…,对每个正整数n,以点Pn为圆心的⊙Pn与x轴及射线y=
在xoy平面上有一系列点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…,对每个正整数n,以点Pn为圆心的⊙Pn与x轴及射线y=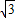 x,(x≥0)都相切,且⊙Pn与⊙Pn+1彼此外切.若x1=1,且xn+1<xn(n∈N*).
x,(x≥0)都相切,且⊙Pn与⊙Pn+1彼此外切.若x1=1,且xn+1<xn(n∈N*).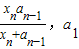 =1,
=1,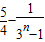 ,(n≥2)
,(n≥2)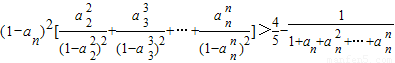 .
.