题目内容
如图,在底面是矩形的四棱锥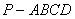 中,
中,
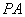 ⊥平面
⊥平面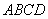 ,
, 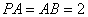 ,
,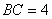 .
.
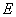 是
是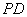 的中点,
的中点,
(Ⅰ)求证:平面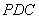 ⊥平面
⊥平面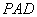 ;
;
(Ⅱ)求二面角 的余弦值;
的余弦值;
(Ⅲ)求直线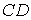 与平面
与平面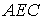 所成角的正弦值
所成角的正弦值
 |
17.解法一:(Ⅰ) ,
, ,
,
 . -------------------------------------------------------------------------------
. -------------------------------------------------------------------------------
 ,
,  .
.
而 ,
,  平面
平面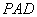
 .
. 
 .
.
(Ⅱ)连结 、
、 ,取
,取 中点
中点 , 连结
, 连结 , 则
, 则 ,
,
∵ 平面
平面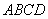 , ∴
, ∴ 平面
平面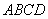 .
.
过 作
作 交
交 于
于 ,连结
,连结 ,
,
则  就是二面角
就是二面角 所成平面角.
所成平面角.
由 ,则
,则 .
.
在 中,
中, 解得
解得
 .
.
因为 是
是 的中点,所以
的中点,所以 .
.
而 ,由勾股定理可得
,由勾股定理可得 .
.
 .
.
(Ⅲ)延长 ,过
,过 作
作 垂直
垂直 于
于 ,连结
,连结 ,
,
又∵ ,∴
,∴ ⊥平面
⊥平面 ,
,
过 作
作 垂直
垂直 于
于 , 则
, 则 ,
,
所以 平面
平面 , 即
, 即 平面
平面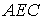 ,
,
所以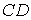 在平面
在平面 内的射影是
内的射影是 ,
, 是直线与平面所成的角.
是直线与平面所成的角.

 .
.

 .
.
 .
.
解法二:以 为原点,
为原点, 所在直线为
所在直线为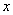 轴,
轴, 所在直线为
所在直线为 轴,
轴, 所在直线为
所在直线为 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则 (0,0,0) ,
(0,0,0) ,  (2,0,0),
(2,0,0),  (2,4,0) ,
(2,4,0) ,  (0,4,0) ,
(0,4,0) ,
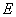 (0,2,1) ,
(0,2,1) ,  (0,0,2) .
(0,0,2) .
∴ =(2,0,0) ,
=(2,0,0) ,  =(0,4,0) ,
=(0,4,0) ,  =(0,0,2) ,
=(0,0,2) ,  =(-2,0,0) ,
=(-2,0,0) ,

 =(0,2,1) ,
=(0,2,1) ,  =(2,4,0) .
=(2,4,0) .
(Ⅰ) ,
,  .
.
又 ,
,  .
.
 ,
,
 ,
,
而 ,
,
∴平面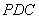 ⊥平面
⊥平面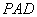 . )
. )
(Ⅱ)设平面 的法向量
的法向量 =
= ,令
,令 ,则
,则 .
.
由 即
即
∴ =
= .
.
平面 的法向量
的法向量 =(0,0,2) ,
=(0,0,2) ,  .
.
所以二面角 所成平面角的余弦值是
所成平面角的余弦值是 .
.
(Ⅲ)因为平面的法向量是 =
= ,而
,而 =(-2,0,0) .
=(-2,0,0) .
所以  .
.
直线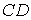 与平面
与平面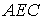 所成角的正弦值
所成角的正弦值  .
.

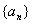 为等比数列,若
为等比数列,若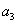 和
和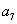 是方程
是方程 +
+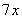 +
+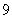 =
=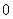 的两个根,则
的两个根,则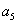 =________.
=________.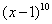 的展开式中
的展开式中 的系数是 .(用数字作答)
的系数是 .(用数字作答) 的正方形
的正方形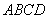 沿对角线
沿对角线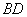 折起,使得平面
折起,使得平面 平面
平面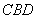 ,形成三棱锥
,形成三棱锥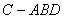 的正视图与俯视图如下图所示,则侧视图的面积为 ( )
的正视图与俯视图如下图所示,则侧视图的面积为 ( )
 B.
B.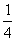 C.
C.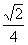 D.
D. 
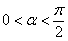 ,
,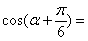
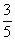 ,则
,则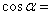 .
.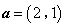 ,
,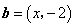 ,若
,若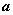 ∥
∥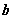 ,则
,则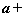
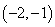 B.
B. C.
C.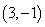 D.
D.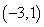
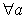 、
、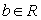 ,运算“
,运算“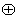 ”、“
”、“ ”定义为:
”定义为: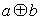 =
=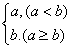 ,
,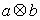 =
=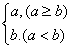 ,则下列各式其中不恒成立的是( )
,则下列各式其中不恒成立的是( )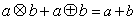 ⑵
⑵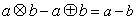
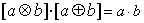 ⑷
⑷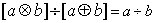
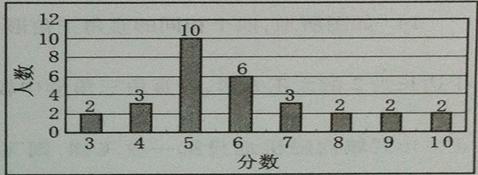
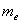 ,众数为
,众数为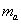 ,平均值为
,平均值为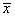 ,则( )
,则( )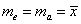 B、
B、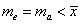 C、
C、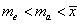 D、
D、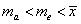
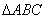 中,角
中,角 满足关系式
满足关系式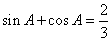 ,则
,则