题目内容
已知f(x)=ax2(a∈R), g(x)=2lnx.
(1)讨论函数F(x)=f(x)-g(x)的单调性;
(2)是否存在实数 a,使得f(x)≥g(x)+2 (x>0)恒成立,若不存在,请说明理由;若存在,求出a的取值范围;
a,使得f(x)≥g(x)+2 (x>0)恒成立,若不存在,请说明理由;若存在,求出a的取值范围;
(3)若方程f(x)=g(x)在区间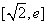 上有两个不相等的实数根,求a的取值范围.
上有两个不相等的实数根,求a的取值范围.
解:(1)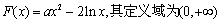
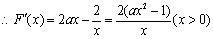
(i)当a>0时,由ax2-1>0得 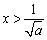 ,
,
由ax2-1<0得  .
.
故当a>0时,F(x)的递增区间为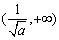 ,
,
递减区间为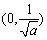 .
.
(ii)当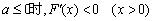 恒成立
恒成立
故当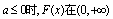 上单调
上单调 递减. ………………………4分
递减. ………………………4分
(2)即使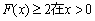 时恒成立.
时恒成立.
(i)当a≤0时,由(1)知当
∴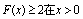 时不可能恒成立.,
时不可能恒成立.,
(ii)当a>0时,由(1)可知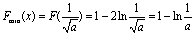
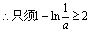 即可 ,
即可 , 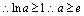
故存在这样的a的值,使得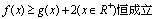
a的取值范围是 ………………………8分
(3)等价 于方程
于方程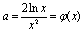 在区间
在区间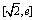 上有两个不等解,
上有两个不等解,
∵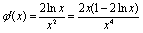
 在区间
在区间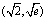 上为增函数,在
上为增函数,在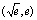 上为减函数,
上为减函数,
∴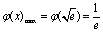 ,
,
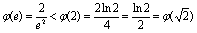 ,
,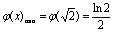
a的取值范围是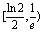

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目

 B.
B.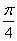 C.
C.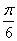 D.
D.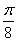
 的正三角形内任一点到三边距离之和为定值
的正三角形内任一点到三边距离之和为定值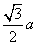 ,类比上述命题,棱长为
,类比上述命题,棱长为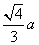 B.
B.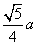 C.
C.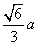 D.
D.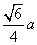
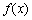 是连续函数,且
是连续函数,且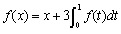 ,则f(x)= .
,则f(x)= .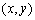 所对应的点都在函数( )
所对应的点都在函数( )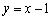 的图象上 B.
的图象上 B.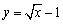 的图象上
的图象上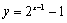 的图象上 D.
的图象上 D.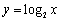 的图象上
的图象上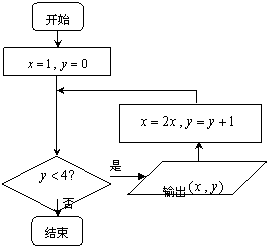
 a,AB⊥AC,D为AA1的中点.
a,AB⊥AC,D为AA1的中点. (Ⅱ)在侧棱BB1上确定一点E,使得二面角E- A1C1一A的大小为
(Ⅱ)在侧棱BB1上确定一点E,使得二面角E- A1C1一A的大小为