题目内容
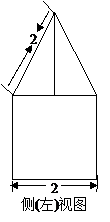
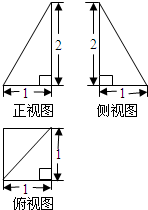
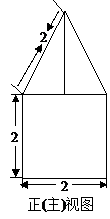一空间几何体的三视图如图所示，则该几何体的体积为（ ）
A . 2
+2
B. 4+ 2
C. 2+ 
D. 2+
C
解析:
由题意可知该几何体为一正四棱锥
与一圆柱拼接而成的,所以该几何体的体
积为这个圆柱的体积与这个正四棱锥的体积
之和,其中圆柱的底面圆直径为2,高为2,所以
圆柱的体积为
;正四棱锥的侧棱长为2,
底面正方形的对角线为2,所以此正四棱锥的
体积为
=
,故选C.
【考点定位】本小题考查了立体几何中的空间想象能力,由三视图能够想象得出空间的立体图形,并能准确地计算出该几何体的体积.
练习册系列答案
阅读快车系列答案
相关题目
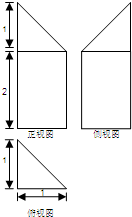
（2013•成都一模）一空间几何体的三视图如图所示，图中各线段旁的数字表示 该线段的长度，则该几何体的体积为（ ）
（2013•德州一模）一空间几何体的三视图如图所示，该几何体的体积为
（2012•厦门模拟）已知一空间几何体的三视图如图所示，则该几何体中相互垂直的棱共有（ ）