题目内容
两个非零向量 不共线,若
不共线,若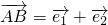 ,
, ,
, ,则三点共线是
,则三点共线是
- A.A、B、C
- B.B、C、D
- C.A、B、D
- D.A、C、D
C
分析:题目给出了三个非零向量, 、
、 、
、 ,明显看出
,明显看出 、
、 不共线,所以先由
不共线,所以先由 求出
求出 ,
,
此时有 ,所以向量
,所以向量 与
与 共线,又两向量过同一点,所以进一步说明三点共线.
共线,又两向量过同一点,所以进一步说明三点共线.
解答:由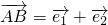 ,
, ,
, ,
,
则 =
= =5
=5 .
.
所以向量 与向量
与向量 共线,又两向量有公共点B,所以A、B、D三点共线.
共线,又两向量有公共点B,所以A、B、D三点共线.
故选C.
点评:本题考查了平面向量的共线问题,解答的关键是共线向量基本定理,即若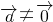 ,则向量
,则向量 与向量
与向量 共线的充要条件是存在实数λ,使
共线的充要条件是存在实数λ,使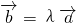 .
.
分析:题目给出了三个非零向量,
 、
、 、
、 ,明显看出
,明显看出 、
、 不共线,所以先由
不共线,所以先由 求出
求出 ,
,此时有
 ,所以向量
,所以向量 与
与 共线,又两向量过同一点,所以进一步说明三点共线.
共线,又两向量过同一点,所以进一步说明三点共线.解答:由
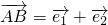 ,
, ,
, ,
,则
 =
= =5
=5 .
.所以向量
 与向量
与向量 共线,又两向量有公共点B,所以A、B、D三点共线.
共线,又两向量有公共点B,所以A、B、D三点共线.故选C.
点评:本题考查了平面向量的共线问题,解答的关键是共线向量基本定理,即若
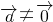 ,则向量
,则向量 与向量
与向量 共线的充要条件是存在实数λ,使
共线的充要条件是存在实数λ,使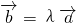 .
. 
练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 不共线.
不共线. 三点是否能构成三角形, 并说明理由.
三点是否能构成三角形, 并说明理由.
 不共线.
不共线. 三点是否能构成三角形, 并说明理由.
三点是否能构成三角形, 并说明理由.
 不共线.
不共线. 三点是否能构成三角形, 并说明理由.
三点是否能构成三角形, 并说明理由.
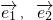 不共线,若
不共线,若 .
. 共线.
共线. 不共线,且
不共线,且 共线,则k的值为( )
共线,则k的值为( )