题目内容
(本小题满分12分)
已知 是等差数列
是等差数列 的前n项和,数列
的前n项和,数列 是等比数列,
是等比数列, 恰为
恰为 的等比中项,圆
的等比中项,圆 ,直线
,直线 ,对任意
,对任意 ,直线
,直线 都与圆C相切.
都与圆C相切.
(I)求数列 的通项公式;
的通项公式;
(II)若 时,
时, 的前n项和为
的前n项和为 ,求证:对任意
,求证:对任意 ,都有
,都有
(1) ,
, ;(2)见解析.
;(2)见解析.
【解析】
试题分析:(1)给出 与
与 的关系,求
的关系,求 ,常用思路:一是利用
,常用思路:一是利用 转化为
转化为 的递推关系,再求其通项公式;二是转化为
的递推关系,再求其通项公式;二是转化为 的递推关系,先求出
的递推关系,先求出 与
与 的关系,再求
的关系,再求 ;由
;由 推
推 时,别漏掉
时,别漏掉 这种情况,大部分学生好遗忘;(2)一般地,如果数列
这种情况,大部分学生好遗忘;(2)一般地,如果数列 是等差数列,
是等差数列, 是等比数列,求数列
是等比数列,求数列
 的前
的前 项的和时,可采用错位相减法求和,一般是和式两边同乘以等比数列
项的和时,可采用错位相减法求和,一般是和式两边同乘以等比数列 的公比,然后做差求解;(3)利用不等式放缩时掌握好规律,怎样从条件证明出结论.
的公比,然后做差求解;(3)利用不等式放缩时掌握好规律,怎样从条件证明出结论.
试题解析:
(Ⅰ) 圆 的圆心为
的圆心为 ,半径为
,半径为 ,对任意
,对任意 ,直线
,直线 都与圆
都与圆 相切.
相切.
所以圆心 到直线
到直线 的距离
的距离 为
为
所以 3分
3分
得
所以 ,
, 4分
4分
当 时,
时,
当 时,
时,
综上,对任意 ,
, 5分
5分
设等比数列 的公比为
的公比为 ,所以
,所以
 恰为
恰为 与
与 的等比中项
的等比中项 ,
, ,所以
,所以
 ,解得
,解得 7分
7分
所以 8分
8分
(Ⅱ)  时,
时,

而 时,
时, 10分
10分

所以
 12分
12分
考点:等差、等比数列的性质及应用.

练习册系列答案
相关题目
 ,则无穷数列
,则无穷数列 前
前 项和的极限为 .
项和的极限为 .  的直线与圆
的直线与圆 有公共点,则该直线的倾斜角的取值范围是
有公共点,则该直线的倾斜角的取值范围是 B.
B.  C.
C.  D.
D. 
 是偶函数,当
是偶函数,当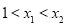 时,
时,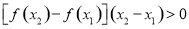 恒成立,设
恒成立,设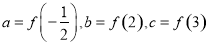 ,则
,则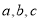 的大小关系为
的大小关系为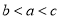 B.
B. 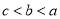 C.
C. 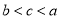 D.
D. 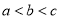
 和圆
和圆 的位置关系为
的位置关系为 的通项公式为
的通项公式为 ,试通过计算
,试通过计算 的值,推测出
的值,推测出 _________.
_________.
 D.
D. 
 的边长为
的边长为 ,
, ,点
,点 分别在边
分别在边 上,
上, .若
.若 ,则
,则
 与
与 的夹角为
的夹角为 ,且
,且 ,那么
,那么 的值为________.
的值为________.