Question

已知F₁（0，-5），F₂（0，5），一双曲线上任意一点M满足||MF₁|-|MF₂||=8，若该曲线的一条渐近线的斜率为k，该曲线的离心率为e，则|k|•e=________．

Answer 1

分析：利用双曲线的定义判断出焦点及实轴长，利用双曲线的三参数的关系b²=c²-a²求出b的值；利用离心率公式及渐近线方程公式求出e及|k|，求出它们的乘积．
解答：据题意知，此双曲线是以F₁，F₂为焦点，且实轴长为8，
所以c=5，a=4，
所以b²=c²-a²=9，所以b=3．
所以；渐近线方程为．
所以|k|=．
所以．
故答案为：．
点评：本题考查双曲线中三个参数的关系：b²=c²-a²注意与椭圆中三个参数的区别、焦点在x轴上的双曲线的渐近线的方程为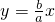；而焦点在y轴时，渐近线的方程为：．