Question

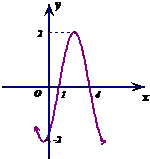（2013•绵阳二模）函数f（x）=Asin（ωx+φ）的部分图象如图所示，则此函数的解析式为（　　）

• A．f(x)=2sin(

  π

  3

  x-

  π

  3

  )
• B．f(x)=2sin(

  π

  6

  x-1)
• C．f(x)=2sin(x-

  π

  3

  )
• D．f(x)=2sin(

  π

  6

  x-

  π

  6

  )

Answer 1

分析：由图可知A，由

T

2

=3可求得ω，由ω×1+φ=0可求得φ．

解答：解：依题意得，A=2，

T

2

=3，
∴T=6，又T=

2π

ω

（ω＞0），
∴ω=

π

3

．
∵f（x）=2sin（

π

3

x+φ）经过（1，0），且改零点的左侧区间与右侧区间均为单调增区间，
∴

π

3

×1+φ=0，
∴φ=-

π

3

．
故选A．

点评：本题考查由y=Asin（ωx+φ）的部分图象确定其解析式，求φ是难点，属于中档题．