题目内容
不等式x2+2x<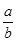 +
+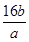 对任意a,b∈(0,+∞)恒成立,则实数x的取值范围是( )
对任意a,b∈(0,+∞)恒成立,则实数x的取值范围是( )
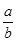 +
+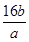 对任意a,b∈(0,+∞)恒成立,则实数x的取值范围是( )
对任意a,b∈(0,+∞)恒成立,则实数x的取值范围是( )| A.(-2,0) | B.(-∞,-2)∪(0,+∞) |
| C.(-4,2) | D.(-∞,-4)∪(2,+∞) |
C
不等式x2+2x<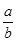 +
+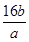 对任意a,b∈(0,+∞)恒成立,等价于x2+2x<
对任意a,b∈(0,+∞)恒成立,等价于x2+2x< min,由于
min,由于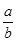 +
+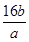 ≥2
≥2 =8(a=4b时等号成立),
=8(a=4b时等号成立),
∴x2+2x<8,解得-4<x<2.
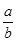 +
+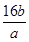 对任意a,b∈(0,+∞)恒成立,等价于x2+2x<
对任意a,b∈(0,+∞)恒成立,等价于x2+2x< min,由于
min,由于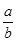 +
+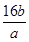 ≥2
≥2 =8(a=4b时等号成立),
=8(a=4b时等号成立),∴x2+2x<8,解得-4<x<2.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 满足
满足 ,则
,则 的最小值为
的最小值为 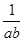 >1
>1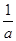 +
+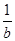 ≤2
≤2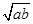 ≥1
≥1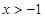 ,则函数
,则函数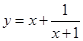 的最小值为( )
的最小值为( )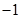
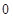
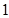
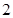
 y2的准线方程是x=1;
y2的准线方程是x=1; ②若x∈R,则
②若x∈R,则 的最小值是2;
的最小值是2; ,且
,且 ,则下列不等式中恒成立的是( )
,则下列不等式中恒成立的是( ) 



 满足
满足 ,则
,则 的最大值___________;
的最大值___________; 的最小值是________.
的最小值是________.