题目内容
【题目】求直线![]() 关于
关于![]() 对称的直线
对称的直线![]() 方程.
方程.
【答案】![]()
【解析】
设![]() 上任意一点
上任意一点![]() 关于
关于![]() 的对称点为
的对称点为![]() 在直线
在直线![]() 上,利用直线
上,利用直线![]() 是
是![]() 的垂直平分线,建立
的垂直平分线,建立![]() 方程关系,将
方程关系,将![]() 用
用![]() 表示,代入直线
表示,代入直线![]() 方程,整理即可;由于
方程,整理即可;由于![]() 相交,可得直线
相交,可得直线![]() 也过该交点,在直线
也过该交点,在直线![]() 再取一点,求出该点关于直线
再取一点,求出该点关于直线![]() 对称点的坐标,且在直线
对称点的坐标,且在直线![]() 上,即可求解;或利用
上,即可求解;或利用![]() 分别与
分别与![]() 夹角相等,设直线
夹角相等,设直线![]() 的斜率为
的斜率为![]() ,确定三直线的方向向量,应用夹角公式建立
,确定三直线的方向向量,应用夹角公式建立![]() 方程,求解即可.
方程,求解即可.
解法1:设![]() 上任意一点
上任意一点![]() 关于
关于![]() 的对称点为
的对称点为![]() ,
,
则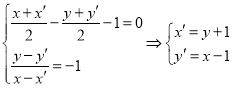 .
.
由于![]() 在直线
在直线![]() 上,
上,
代入得![]() 即
即![]() .
.
解法2:由![]() .故
.故![]() 与
与![]() 交点坐标为
交点坐标为![]() .
.
另取![]() 上不同于
上不同于![]() 的一点
的一点![]() ,设
,设![]() 关于
关于![]() 的对称点
的对称点![]() ,则
,则
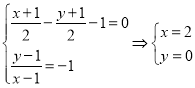 ,即点
,即点![]() 坐标为
坐标为![]() .
.
所以,过![]() 与
与![]() 的直线
的直线![]() 的方程为
的方程为![]() ,
,
即![]() .
.
解法3:由![]() .故
.故![]() 与
与![]() 交点坐标为
交点坐标为![]() .
.
设直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() 的一个方向向量为
的一个方向向量为![]() ,
,
又直线![]() 一个方向向量为
一个方向向量为![]() ,直线
,直线![]() 的一个方向向量为
的一个方向向量为![]() ,
,
则![]() (舍),
(舍),![]() .
.
所以,直线![]() 的方程为
的方程为![]() ,即
,即![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目