题目内容
【题目】已知某正三棱锥的底面边长为4,侧面与底面所成二面角的余弦值为![]() ,球
,球![]() 为该三棱锥的内切球.球
为该三棱锥的内切球.球![]() 与球
与球![]() 相切,且与该三棱锥的三个侧面也相切,则球
相切,且与该三棱锥的三个侧面也相切,则球![]() 与球
与球![]() 的表面积之比为( )
的表面积之比为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
先利用侧面与底面所成二面角的余弦值为![]() 可得三个侧面的等腰三角形底边上的高,再根据等体积法可求得球
可得三个侧面的等腰三角形底边上的高,再根据等体积法可求得球![]() 的半径,进而根据立体几何中的相似,可得
的半径,进而根据立体几何中的相似,可得![]() 所切的三棱锥的相似比,进而得到
所切的三棱锥的相似比,进而得到![]() 的半径比以及表面积的比.
的半径比以及表面积的比.
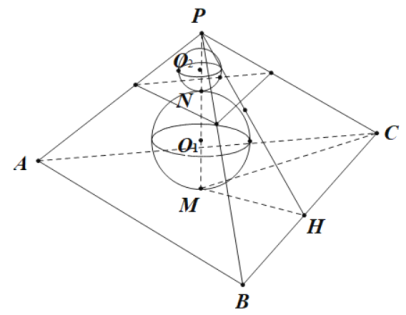
如图,正三棱锥![]() ,设
,设![]() 在底面
在底面![]() 上的投影为
上的投影为![]() ,取
,取![]() 中点
中点![]() ,易得
,易得![]() ,
,![]() ,
,![]() 即为侧面与底面所成二面角.
即为侧面与底面所成二面角.
又![]() ,故
,故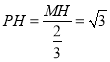 ,
,![]() .
.
设球![]() 的半径为
的半径为![]() ,则
,则![]() ,即
,即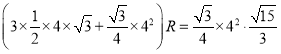 ,解得
,解得![]() .
.
根据题意可知,![]() 为与正三棱锥
为与正三棱锥![]() 相似的正三棱锥的内切球,且该三棱锥的高
相似的正三棱锥的内切球,且该三棱锥的高![]() .故两正三棱锥的相似比为
.故两正三棱锥的相似比为![]() ,故其内切球的
,故其内切球的![]() 的半径比也为
的半径比也为![]() ,故球
,故球![]() 与球
与球![]() 的表面积之比为
的表面积之比为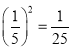 .
.
故选:D

练习册系列答案
相关题目