题目内容
设θ∈(
,π),则直线xcosθ+ysinθ+1=0的倾斜角α为
| π |
| 2 |
θ-
| π |
| 2 |
θ-
.| π |
| 2 |
分析:根据直线xcosθ+ysinθ+1=0的斜率为 tanα=-
=tan(θ-
),θ-
∈(0,
),且α∈[0,π),可得 θ-
=α,从而得出结论.
| cosθ |
| sinθ |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
解答:解:由于直线xcosθ+ysinθ+1=0的斜率为 tanα=-
=-cotθ=tan(θ-
),
再由 θ∈(
,π),可得θ-
∈(0,
).
再由α∈[0,π),可得 θ-
=α,
故答案为 θ-
.
| cosθ |
| sinθ |
| π |
| 2 |
再由 θ∈(
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
再由α∈[0,π),可得 θ-
| π |
| 2 |
故答案为 θ-
| π |
| 2 |
点评:本题主要考查直线的斜率和倾斜角,诱导公式的应用,属于基础题.

练习册系列答案
相关题目
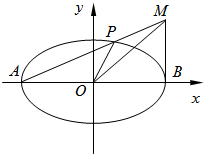 如图,已知椭圆
如图,已知椭圆