题目内容
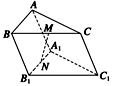
△ABC和△A1B1C1所在的平面交于直线l,AB和A1B1交于P,BC和B1C1交于Q,AC和A1C1交于R,则下列判断正确的是
- A.P、Q、R确定平面r,且l?r
- B.P、Q、R确定平面r,且l∥r
- C.P、Q、R确定平面r,且l⊥r
- D.P、Q、R都在直线l上
D
分析:首先说明P、Q、R为△ABC和△A1B1C1的公共点,再由公理二得出P、Q、R都在直线l上.
解答:因为AB和A1B1交于P,所以P∈AB,P∈A1B1,所以P∈面ABC且P∈面A1B1C1,
因为△ABC和△A1B1C1所在的平面交于直线l,所以P∈l.
同理Q∈l,R∈l,所以P、Q、R都在直线l上
故选D
点评:本题考查平面的性质及应用,考查逻辑推理能力.证明三点共线问题一般思路为:证明点是两个平面的公共点,由公理二,公共点一定在两个平面的交线上.
分析:首先说明P、Q、R为△ABC和△A1B1C1的公共点,再由公理二得出P、Q、R都在直线l上.
解答:因为AB和A1B1交于P,所以P∈AB,P∈A1B1,所以P∈面ABC且P∈面A1B1C1,
因为△ABC和△A1B1C1所在的平面交于直线l,所以P∈l.
同理Q∈l,R∈l,所以P、Q、R都在直线l上
故选D
点评:本题考查平面的性质及应用,考查逻辑推理能力.证明三点共线问题一般思路为:证明点是两个平面的公共点,由公理二,公共点一定在两个平面的交线上.

练习册系列答案
 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
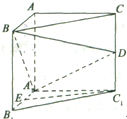 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面A1B1C1,∠B1A1C1=90°,D、E分别为CC1和A1B1的中点,且A1A=AC=2AB=2.
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面A1B1C1,∠B1A1C1=90°,D、E分别为CC1和A1B1的中点,且A1A=AC=2AB=2.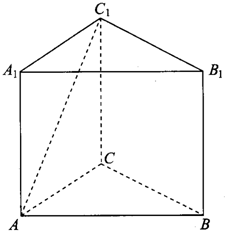 如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=AA1=2
如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=AA1=2 如图,△ABC和△A1AC是正三角形,平面A1AC⊥底面ABC,A1B1⊥∥AB,A1B1=AB=2,
如图,△ABC和△A1AC是正三角形,平面A1AC⊥底面ABC,A1B1⊥∥AB,A1B1=AB=2,