题目内容
如图所示,在三棱柱ABC—A1B1C1中,M、N分别是BC和A1B1的中点.
求证:MN∥平面AA1C1.
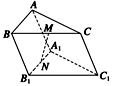
证明略
解析:
设A1C1中点为F,连接NF,FC,
∵N为A1B1中点,
∴NF∥B1C1,且NF=![]() B1C1,
B1C1,
又由棱柱性质知B1C1![]() ?? BC,
?? BC,
又M是BC的中点,
 ∴NF
∴NF![]() ?? MC,
?? MC,
∴四边形NFCM为平行四边形.
∴MN∥CF,又CF![]() 平面AA1C1,
平面AA1C1,
MN![]() 平面AA1C1,
平面AA1C1,
∴MN∥平面AA1C1.

练习册系列答案
相关题目
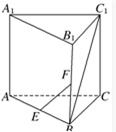 如图所示,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点E、F分别是棱AB、BB1的中点,则直线EF和BC1所成的角是( )
如图所示,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点E、F分别是棱AB、BB1的中点,则直线EF和BC1所成的角是( )| A、45° | B、60° | C、90° | D、120° |
 如图所示,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心
如图所示,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心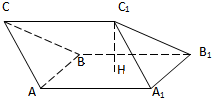 如图所示,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心
如图所示,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心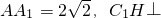 平面AA1B1B且
平面AA1B1B且 .
.
