题目内容
已知椭圆: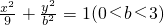 ,左右焦点分别为F1,F2,过F1的直线l交椭圆于A,B两点,则
,左右焦点分别为F1,F2,过F1的直线l交椭圆于A,B两点,则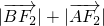 的最大值为________.
的最大值为________.

分析:如图所示,利用椭圆的定义得到
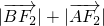 =12-
=12- .因此只有当
.因此只有当 取得最小值时,
取得最小值时,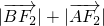 取得最大值,分AB⊥x轴和AB与x轴不垂直两种情况讨论,当AB与x轴不垂直时,利用弦长公式即可得出,通过比较得到
取得最大值,分AB⊥x轴和AB与x轴不垂直两种情况讨论,当AB与x轴不垂直时,利用弦长公式即可得出,通过比较得到 的最小值.
的最小值.解答:如图所示,
由椭圆的定义可知:
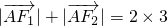 =
= ,
,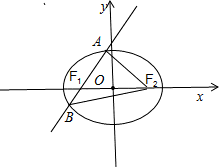
∴
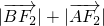 =12-
=12- .好
.好当AB⊥x轴时,把x=-c代入椭圆的方程得
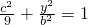 ,解得
,解得 ,
,此时,
 ,则
,则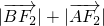 =12-
=12- =
= ;
;当直线AB与x轴不垂直时,设直线AB的方程为y=k(x+c),A(x1,y1),
B(x2,y2).
联立
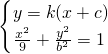 ,消去y得到(b2+9k2)x2+18k2cx+9k2c2-9b2=0,
,消去y得到(b2+9k2)x2+18k2cx+9k2c2-9b2=0,∴
 ,
,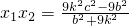 ,
,∴
 =
=
=
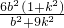
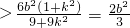 .
.综上可知:只有当AB⊥x轴时,
 取得最小值,此时
取得最小值,此时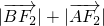 取得最大值
取得最大值 .
.故答案为
 .
.点评:熟练掌握椭圆的定义、分类讨论的思想方法、直线与圆锥曲线相交时的弦长公式的应用是解题的关键.

练习册系列答案
相关题目
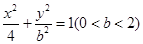 ,左右焦点分别为
,左右焦点分别为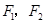 ,过
,过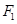 的直线
的直线 交椭圆于
交椭圆于 两点,若
两点,若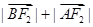 的最大值为5,则
的最大值为5,则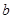 的值是( )
的值是( )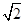 C.
C.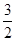 D.
D.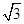
 ,直线
,直线 与椭圆C交于不同的两点M,N,以线段MN为直径作圆P。
与椭圆C交于不同的两点M,N,以线段MN为直径作圆P。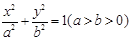 的左右焦点分别为
的左右焦点分别为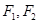 ,离心率为
,离心率为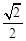 ,两焦点与上下顶点形成的菱形面积为2.
,两焦点与上下顶点形成的菱形面积为2.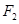 的直线
的直线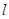 与椭圆交于A, B两点,四边形
与椭圆交于A, B两点,四边形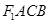 为平行四边形,
为平行四边形,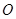 为坐标原点,且
为坐标原点,且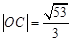 ,求直线
,求直线