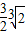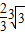题目内容
函数f(t)=∫1t 在(0,+∞)的最小值为
在(0,+∞)的最小值为
- A.0
- B.

- C.

- D.

D
分析:先由f(t)=∫1t ,根据定积分的运算规则,解出f(t),根据函数的解析式解出它在(0,+∞)的最小值
,根据定积分的运算规则,解出f(t),根据函数的解析式解出它在(0,+∞)的最小值
解答:f(t)=∫1t =
= =
= -2=
-2= -2
-2
又t∈(0,+∞),故f(t)= -2≥3
-2≥3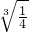 -2=
-2=
等号当且仅当 时成立
时成立
故选D
点评:本题考查定积分,利用基本不等式求函数的最值,解题的关键是熟练掌握求定积分的方法以及根据函数的形式选择求最值的方法,本题的难点是根据所得出的函数的形式选择求最值的方法,本题求解时用的三元基本不等式,新教材地区的学生就不要做本题了
分析:先由f(t)=∫1t
 ,根据定积分的运算规则,解出f(t),根据函数的解析式解出它在(0,+∞)的最小值
,根据定积分的运算规则,解出f(t),根据函数的解析式解出它在(0,+∞)的最小值解答:f(t)=∫1t
 =
= =
= -2=
-2= -2
-2又t∈(0,+∞),故f(t)=
 -2≥3
-2≥3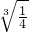 -2=
-2=
等号当且仅当
 时成立
时成立故选D
点评:本题考查定积分,利用基本不等式求函数的最值,解题的关键是熟练掌握求定积分的方法以及根据函数的形式选择求最值的方法,本题的难点是根据所得出的函数的形式选择求最值的方法,本题求解时用的三元基本不等式,新教材地区的学生就不要做本题了

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
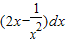 在(0,+∞)的最小值为( )
在(0,+∞)的最小值为( )