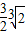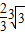题目内容
函数f（t）=∫1t(2x-
)dx在（0，+∞）的最小值为（ ）
| 1 |
| x2 |
| A．0 | B．
| C．
| D．
|
f（t）=∫1t(2x-
)dx=
=t2+
-2=t2+
+
-2
又t∈（0，+∞），故f（t）=t2+
+
-2≥3
-2=
-2
等号当且仅当t2=
时成立
故选D
| 1 |
| x2 |
(x2+
| t1 |
| 1 |
| t |
| 1 |
| 2t |
| 1 |
| 2t |
又t∈（0，+∞），故f（t）=t2+
| 1 |
| 2t |
| 1 |
| 2t |
| 3 |
| ||
| 3 |
| 2 |
| 3 | 2 |
等号当且仅当t2=
| 1 |
| 2t |
故选D
练习册系列答案
相关题目
在（0，+∞）的最小值为
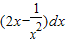在（0，+∞）的最小值为（ ）
