题目内容
2.函数f(x)=$\sqrt{3}$sinx+cos($\frac{π}{3}$+x)的最大值为1.分析 由三角函数公式化简为一个角一个函数的形式,由振幅的意义可得.
解答 解:由三角函数公式化简可得
f(x)=$\sqrt{3}$sinx+cos($\frac{π}{3}$+x)
=$\sqrt{3}$sinx+cos$\frac{π}{3}$cosx-sin$\frac{π}{3}$sinx
=$\sqrt{3}$sinx+$\frac{1}{2}$cosx-$\frac{\sqrt{3}}{2}$sinx
=$\frac{1}{2}$cosx+$\frac{\sqrt{3}}{2}$sinx
=cos$\frac{π}{3}$cosx+sin$\frac{π}{3}$sinx
=cos(x-$\frac{π}{3}$)
∴函数的最大值为:1
故答案为:1
点评 本题考查三角函数的最值,涉及和差角的三角函数公式,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.已知随机变量ξ的分布列如下:
则P(2≤ξ<4)=0.6.
| ξ | 1 | 2 | 3 | 4 | 5 |
| P | 0.1 | 0.2 | 0.4 | 0.2 | 0.1 |
17.已知随机变量ξ的分布列为
分别求出随机变量η1=$\frac{1}{2}$ξ,η2=ξ2的分布列.
| ξ | -2 | -1 | 0 | 1 | 2 | 3 |
| P | $\frac{1}{12}$ | $\frac{3}{12}$ | $\frac{4}{12}$ | $\frac{1}{12}$ | $\frac{2}{12}$ | $\frac{1}{12}$ |
12.定义在R上的偶函数f (x)满足:对任意的x1、x2∈(-∞,0]( x1≠x2),有(x2-x1)[f (x2)-f (x1)]>0,则当n∈N*时,有( )
| A. | f (-n)<f (n-1)<f (n+1) | B. | f (n+1)<f (-n)<f (n-1) | ||
| C. | f (n-1)<f (-n)<f (n+1) | D. | f (n+1)<f (n-1)<f (-n) |
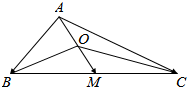 如图,在△ABC中,O为中线AM上的动点.
如图,在△ABC中,O为中线AM上的动点.