题目内容
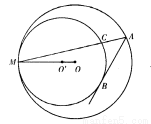
22、如图，⊙O内切于△ABC的边于D，E，F，AB=AC，连接AD交⊙O于点H，直线HF交BC的延长线于点G．（1）求证：圆心O在直线AD上．
（2）求证：点C是线段GD的中点．
分析：切线PA和PB，切点分别是A和B根据切线的性质和圆周角定理，四边形内角和是360度即可求得劣弧AB的度数．
解答：
证明：（1）∵AB=AC，AF=AE
∴CD=BE
又∵CF=CD，BD=BE
∴CD=BD
又∵△ABC是等腰三角形，
∴AD是∠CAB的角分线
∴圆心O在直线AD上．（5分）
（II）连接DF，由（I）知，DH是⊙O的直径，
∴∠DHF=90°，∴∠FDH+∠FHD=90°
又∵∠G+∠FHD=90°
∴∠FDH=∠G
∵⊙O与AC相切于点F
∴∠AFH=∠GFC=∠FDH
∴∠GFC=∠G
∴CG=CF=CD
∴点C是线段GD的中点．（10分）
证明：（1）∵AB=AC，AF=AE∴CD=BE
又∵CF=CD，BD=BE
∴CD=BD
又∵△ABC是等腰三角形，
∴AD是∠CAB的角分线
∴圆心O在直线AD上．（5分）
（II）连接DF，由（I）知，DH是⊙O的直径，
∴∠DHF=90°，∴∠FDH+∠FHD=90°
又∵∠G+∠FHD=90°
∴∠FDH=∠G
∵⊙O与AC相切于点F
∴∠AFH=∠GFC=∠FDH
∴∠GFC=∠G
∴CG=CF=CD
∴点C是线段GD的中点．（10分）
点评：本题利用了切线的性质，四边形的内角和为360度及圆周角定理求解．
练习册系列答案
相关题目
10、如图⊙O内切于△ABC，切点分别为D、E、F；若∠ABC=40°，∠ACB=60°，连接OE、OF，则∠EOF为（ ）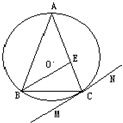
（1）已知点A是曲线ρ=2sinθ上任意一点，则点A到直线
10、如图，△ABC内接于圆⊙O，CT切⊙O于C，∠ABC=100°，∠BCT=40°，则∠AOB=（ ）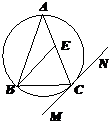
如图：△ABC内接于⊙O，AB=AC，直线MN切⊙O于点C，BE∥MN交AC于点E，若AB=6，BC=4，则AE的长为（ ）
的值．