题目内容
数列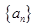 中,已知
中,已知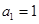 ,
,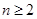 时,
时,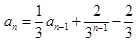 .数列
.数列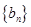 满足:
满足: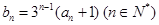 .
.
(1)证明: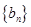 为等差数列,并求
为等差数列,并求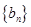 的通项公式;
的通项公式;
(2)记数列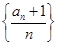 的前
的前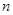 项和为
项和为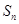 ,若不等式
,若不等式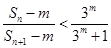 成立(
成立(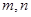 为正整数).求出所有符合条件的有序实数对
为正整数).求出所有符合条件的有序实数对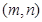 .
.
【答案】
(1)通项公式 ,(2) 有序实数对
,(2) 有序实数对
【解析】
试题分析:(1)由等差数列的定义证明, 当 时,
时, 经过整理为一个常数,从而得出它的公差,进一步得出它的通项公式.
经过整理为一个常数,从而得出它的公差,进一步得出它的通项公式.
(2)利用(1)的结论, 可得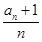 表示的式子,经判断
表示的式子,经判断 为等比数列,利用等比数列的前n项和公式求出
为等比数列,利用等比数列的前n项和公式求出 ,表示出
,表示出 为多少,利用不等式得出m的范围,进一步得出有序实数对.
为多少,利用不等式得出m的范围,进一步得出有序实数对.
试题解析:(Ⅰ) 时,
时, , 2分
, 2分
代入 整理得
整理得 ,
,
故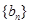 是公差为
是公差为 的等差数列. 6分
的等差数列. 6分
通项公式
(Ⅱ)由(Ⅰ)得, ,故
,故 ,所以
,所以 8分
8分
则 10分
10分
因为 ,得
,得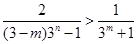 11分
11分
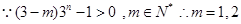 12分
12分
当 时,
时, ;当
;当 时,
时, 13分
13分
综上,存在符合条件的所有有序实数对 为:
为: . 14分
. 14分
考点:等差数列,等比数列,不等式.

练习册系列答案
相关题目
在数列{an}中,已知a1=1,且当n≥2时,a1a2…an=n2,则a3+a5等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 中,已知
中,已知 ,则前
,则前 项和
项和 取最大值时所对应的项数
取最大值时所对应的项数 中,已知通项公式为
中,已知通项公式为 ,则当n为何值时,该数列的前n项和
,则当n为何值时,该数列的前n项和 取得最大值?最大值是多少?
取得最大值?最大值是多少?