题目内容
(本大题满分12分)
给出定义在 上的三个函数:
上的三个函数: ,已知
,已知 处取极值.
处取极值.
(I)确定函数 的单调性;
的单调性;
(II)求证:当 成立.
成立.
(III)把函数 的图象向上平移6个单位得到函数
的图象向上平移6个单位得到函数 的图象,试确定函数
的图象,试确定函数 的零点个数,并说明理由。
的零点个数,并说明理由。
【答案】

略
【解析】(I)由题设, …………1分
…………1分
由已知, …………2分
…………2分
于是 …………3分
…………3分
由
所以 上是增函数,在(0,1)上是减函数。 …………4分
上是增函数,在(0,1)上是减函数。 …………4分
(II)当 时,
时, …………5分
…………5分
欲证
即证 …………6分
…………6分

所以 上为增函数。 …………7分
上为增函数。 …………7分
从而当
 …………8分
…………8分
(III)由题设,
则
即 …………9分
…………9分
|

在(0,4)上是减函数。 …………10分

由图可知,当 时,两个函数图象有2个交点,
时,两个函数图象有2个交点,
故函数 有2个零点。 …………12分
有2个零点。 …………12分

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目

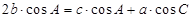 ,
,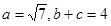 ,求△ABC的面积.
,求△ABC的面积.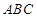 中,
中,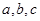 分别为内角
分别为内角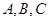 的对边,且
的对边,且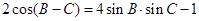
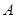
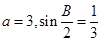 ,求
,求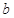
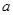 为实常数,函数
为实常数,函数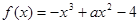 ,
,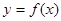 的图象在点
的图象在点 处的切线的倾斜角为
处的切线的倾斜角为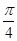 ,求函数
,求函数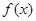 的单调区间;
的单调区间;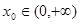 ,使
,使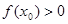 ,求
,求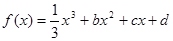 的图象过点(0,3),且在
的图象过点(0,3),且在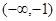 和
和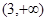 上为增
上为增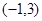 上为减函数.
上为减函数.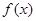 的解析式;
的解析式;