题目内容
等腰三角形的周长为
，问绕这个三角形的底边旋转一周所成的几何体的体积最大时，各边长分别是多少？
，问绕这个三角形的底边旋转一周所成的几何体的体积最大时，各边长分别是多少？当腰长为
时，底边长为
时，所求旋转体的体积最大。
时，底边长为时，所求旋转体的体积最大。设等腰三角形腰长为
，则底边长为
，绕三角形的底边转一围所成的几何体是两个相等圆锥的组合体，圆锥的高为
，底面半径
，则圆锥体的体积为
，所求组合体的体积为
，∴
。令
得，这是定义域内的唯一的极值点，因此当腰长为时，底边长为时，所求旋转体的体积最大。
，则底边长为，绕三角形的底边转一围所成的几何体是两个相等圆锥的组合体，圆锥的高为，底面半径，则圆锥体的体积为，所求组合体的体积为，∴。令得，这是定义域内的唯一的极值点，因此当腰长为时，底边长为时，所求旋转体的体积最大。
练习册系列答案
灵星计算小达人系列答案
孟建平错题本系列答案
相关题目
的图象过点P（0，2），且在点M（－1，f（－1））处的切线方程为
. （Ⅰ）求函数
的解析式；
的另一点A，问电灯与点0的距离怎样，可使点A处有最大的照度？（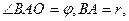
照度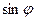与
成正比，与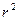
成反比）
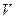的圆柱形水池，已知底的单位面积造价是侧面单位造价的一半，问：如何设计水池的底半径和高，才能使总造价最省？
（百件）的总成本函数为
（万元），总收益函数为
（万元），则生产这种商品所获利润的最大值为 。此时生产这种商品 百件。
与曲线
相切，试求
的值。
的正六边形纸板剪去相同的六个角，做成一个底面为正六边形的无盖六棱柱盒子，设高为
，所做成的盒子体积为
（不计接缝）。
为多少时，体积
在点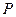
处切线的斜率为
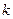，当
时，点
（米）与时间
（秒）间的函数关系式
，则它在第
秒末的瞬时速度是 。