题目内容
(理)(1)证明不等式:ln(1+x)<
(x>0).
(2)已知函数f(x)=ln(1+x)-
在(0,+∞)上单调递增,求实数a的取值范围.
(3)若关于x的不等式
+
≥1在[0,+∞)上恒成立,求实数b的最大值.
| x | ||
|
(2)已知函数f(x)=ln(1+x)-
| ax |
| a+x |
(3)若关于x的不等式
| x |
| 1+bx |
| 1 |
| ex |
(1)证明:(1)令h(x)=ln(1+x)-
,则h′(x)=
<0
∴h(x)在(0,+∞)上单调递减,即h(x)<h(0)=0
∴ln(1+x)-
<0
∴ln(1+x)<
(x>0).
(2)求导函数,可得f′(x)=
,令f′(x)=0,可得x=0或x=a2-2a,
∵函数f(x)=ln(1+x)-
在(0,+∞)上单调递增
∴f′(x)≥0在(0,+∞)上恒成立
∴a2-2a≤0
∵f(x)在(0,+∞)上有意义
∴a≥0
∴0≤a≤2;
(3)关于x的不等式
+
≥1在[0,+∞)上恒成立,等价于
≥1-
在[0,+∞)上恒成立,
∵1-
≥0,∴b≥0
当x>0时,b≤1+
-
构造函数g(x)=1+
-
,则g′(x)=-
+
由(1)知,ln(1+x)<
(x>0).
以ex代1+x,可得x<
,
∵x>0,∴-
+
>0,
∴g′(x)>0,
∴g(x)在(0,+∞)上单调增
当x>0且x→0时,g(x)→1
∴b≤1
∴实数b的最大值为1
| x | ||
|
1-
| ||||||
| 1+x |
∴h(x)在(0,+∞)上单调递减,即h(x)<h(0)=0
∴ln(1+x)-
| x | ||
|
∴ln(1+x)<
| x | ||
|
(2)求导函数,可得f′(x)=
| x[x-(a2-2a)] |
| (x+1)(x+a)2 |
∵函数f(x)=ln(1+x)-
| ax |
| a+x |
∴f′(x)≥0在(0,+∞)上恒成立
∴a2-2a≤0
∵f(x)在(0,+∞)上有意义
∴a≥0
∴0≤a≤2;
(3)关于x的不等式
| x |
| 1+bx |
| 1 |
| ex |
| x |
| 1+bx |
| 1 |
| ex |
∵1-
| 1 |
| ex |
当x>0时,b≤1+
| 1 |
| ex-1 |
| 1 |
| x |
构造函数g(x)=1+
| 1 |
| ex-1 |
| 1 |
| x |
| ex |
| (ex-1)2 |
| 1 |
| x2 |
由(1)知,ln(1+x)<
| x | ||
|
以ex代1+x,可得x<
| ex-1 | ||
|
∵x>0,∴-
| ex |
| (ex-1)2 |
| 1 |
| x2 |
∴g′(x)>0,
∴g(x)在(0,+∞)上单调增
当x>0且x→0时,g(x)→1
∴b≤1
∴实数b的最大值为1

练习册系列答案
相关题目
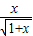 (x>0).
(x>0).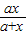 在(0,+∞)上单调递增,求实数a的取值范围.
在(0,+∞)上单调递增,求实数a的取值范围.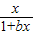
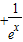 ≥1在[0,+∞)上恒成立,求实数b的最大值.
≥1在[0,+∞)上恒成立,求实数b的最大值.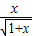 (x>0).
(x>0). 在(0,+∞)上单调递增,求实数a的取值范围.
在(0,+∞)上单调递增,求实数a的取值范围.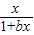
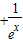 ≥1在[0,+∞)上恒成立,求实数b的最大值.
≥1在[0,+∞)上恒成立,求实数b的最大值.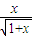 (x>0).
(x>0).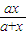 在(0,+∞)上单调递增,求实数a的取值范围.
在(0,+∞)上单调递增,求实数a的取值范围.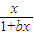
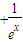 ≥1在[0,+∞)上恒成立,求实数b的最大值.
≥1在[0,+∞)上恒成立,求实数b的最大值.