题目内容
已知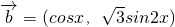 ,
,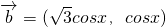 ,设函数f(x)=
,设函数f(x)= (x∈R)
(x∈R)
(1)求f(x)的最小正周期及单调递增区间;
(2)当x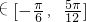 时,求f(x)的值域.
时,求f(x)的值域.
解:(1)∵f(x)= =
= =sin(2x+
=sin(2x+ )+
)+ ,∴f(x)的最小正周期为π.
,∴f(x)的最小正周期为π.
由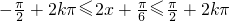 得,-
得,-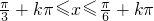 ,(k∈Z),解得
,(k∈Z),解得 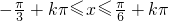 ,
,
故f(x)的单调增区间为[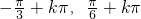 ],(k∈Z).
],(k∈Z).
(2)由(1)知f(x)=sin(2x+ )+
)+ ,又当 x
,又当 x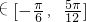 ,2x+
,2x+
 ,故
,故 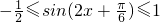 ,
,
从而 f(x)的值域为[0, ].
].
分析:(1)将函数化简为单一函数,f(x)= =(
=(  =sin(2x+
=sin(2x+ )+
)+ ,然后运用周期公式得到结论.
,然后运用周期公式得到结论.
(2)由(1)知f(x)=sin(2x+ )+
)+ ,结合定义域求解得到x
,结合定义域求解得到x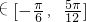 ,2x+
,2x+
 ,根据函数图象得到结论.
,根据函数图象得到结论.
点评:本试题主要是考查了两个向量的数量积公式,正弦函数的周期性、单调性、定义域和值域,属于中档题.
 =
= =sin(2x+
=sin(2x+ )+
)+ ,∴f(x)的最小正周期为π.
,∴f(x)的最小正周期为π. 由
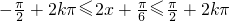 得,-
得,-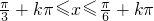 ,(k∈Z),解得
,(k∈Z),解得 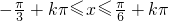 ,
,故f(x)的单调增区间为[
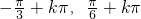 ],(k∈Z).
],(k∈Z). (2)由(1)知f(x)=sin(2x+
 )+
)+ ,又当 x
,又当 x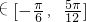 ,2x+
,2x+
 ,故
,故 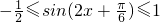 ,
,从而 f(x)的值域为[0,
 ].
].分析:(1)将函数化简为单一函数,f(x)=
 =(
=(  =sin(2x+
=sin(2x+ )+
)+ ,然后运用周期公式得到结论.
,然后运用周期公式得到结论.(2)由(1)知f(x)=sin(2x+
 )+
)+ ,结合定义域求解得到x
,结合定义域求解得到x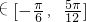 ,2x+
,2x+
 ,根据函数图象得到结论.
,根据函数图象得到结论.点评:本试题主要是考查了两个向量的数量积公式,正弦函数的周期性、单调性、定义域和值域,属于中档题.

练习册系列答案
相关题目
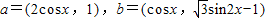 ,设函数f(x)=a•b,其中x∈R.
,设函数f(x)=a•b,其中x∈R.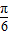 个单位得到g(x)的图象,求g(x)的解析式.
个单位得到g(x)的图象,求g(x)的解析式. ,设函数f(x)=
,设函数f(x)= ,
, ,f(x)=
,f(x)= ,求cosx的值;
,求cosx的值; a,求f(B)的取值范围。
a,求f(B)的取值范围。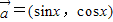 ,
,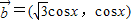 ,设函数f(x)=
,设函数f(x)=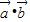 (x∈R)
(x∈R)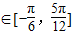 时,求f(x)的值域.
时,求f(x)的值域.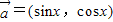 ,
,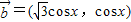 ,设函数f(x)=
,设函数f(x)=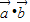 (x∈R)
(x∈R)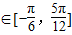 时,求f(x)的值域.
时,求f(x)的值域.