题目内容
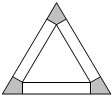 把边长为a的等边三角形铁皮剪去三个相同的四边形(如图阴影部分)后,用剩余部分做成一个无盖的正三棱柱形容器(不计接缝),设容器的高为x,容积为V(x).
把边长为a的等边三角形铁皮剪去三个相同的四边形(如图阴影部分)后,用剩余部分做成一个无盖的正三棱柱形容器(不计接缝),设容器的高为x,容积为V(x).(Ⅰ)写出函数V(x)的解析式,并求出函数的定义域;
(Ⅱ)求当x为多少时,容器的容积最大?并求出最大容积.
分析:(Ⅰ)根据容器的高为x,求得做成的正三棱柱形容器的底边长,从而可得函数V(x)的解析式,函数的定义域;
(Ⅱ)实际问题归结为求函数V(x)在区间(0,
a)上的最大值点,先求V(x)的极值点,再确定极大值就是最大值即可.
(Ⅱ)实际问题归结为求函数V(x)在区间(0,
| ||
| 6 |
解答:解:(Ⅰ)因为容器的高为x,则做成的正三棱柱形容器的底边长为(a-2
x)----(1分).
则V(x)=
(a-2
x)2x.-------------------------(3分)
函数的定义域为(0,
a).-------------------------(4分)
(Ⅱ)实际问题归结为求函数V(x)在区间(0,
a)上的最大值点.
先求V(x)的极值点.
在开区间(0,
a)内,V′(x)=9
x2-6ax+
a2--------------------(6分)
令V'(x)=0,即令9
x2-6ax+
a2=0,解得x1=
a,x2=
a(舍去).
因为x1=
a在区间(0,
a)内,x1可能是极值点.
当0<x<x1时,V'(x)>0;当x1<x<
a时,V'(x)<0.---------------------(8分)
因此x1是极大值点,且在区间(0,
a)内,x1是唯一的极值点,
所以x=x1=
a是V(x)的最大值点,并且最大值 f(
a)=
a3
即当正三棱柱形容器高为
a时,容器的容积最大为
a3.-------------------(10分)
| 3 |
则V(x)=
| ||
| 4 |
| 3 |
函数的定义域为(0,
| ||
| 6 |
(Ⅱ)实际问题归结为求函数V(x)在区间(0,
| ||
| 6 |
先求V(x)的极值点.
在开区间(0,
| ||
| 6 |
| 3 |
| ||
| 4 |
令V'(x)=0,即令9
| 3 |
| ||
| 4 |
| ||
| 18 |
| ||
| 6 |
因为x1=
| ||
| 18 |
| ||
| 6 |
当0<x<x1时,V'(x)>0;当x1<x<
| ||
| 6 |
因此x1是极大值点,且在区间(0,
| ||
| 6 |
所以x=x1=
| ||
| 18 |
| ||
| 18 |
| 1 |
| 54 |
即当正三棱柱形容器高为
| ||
| 18 |
| 1 |
| 54 |
点评:本题考查函数模型的构建,考查导数知识的运用,解题的关键是求出体积,利用导数知识求解.单峰函数,极值就是最值.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 我们把由半椭圆
我们把由半椭圆 我们把由半椭圆
我们把由半椭圆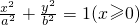 与半椭圆
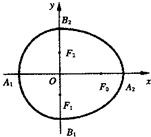
与半椭圆 合成的曲线称作“果圆”(其中a2=b2+c2,a>b>c>0).如图,设点F0,F1,F2是相应椭圆的焦点,A1、A2和B1、B2是“果圆”与x,y轴的交点,若△F0F1F2是边长为1的等边三角,则a,b的值分别为
合成的曲线称作“果圆”(其中a2=b2+c2,a>b>c>0).如图,设点F0,F1,F2是相应椭圆的焦点,A1、A2和B1、B2是“果圆”与x,y轴的交点,若△F0F1F2是边长为1的等边三角,则a,b的值分别为


 与半椭圆
与半椭圆 合成的曲线称作“果圆”(其中a2=b2+c2,a>b>c>0).如图,设点F,F1,F2是相应椭圆的焦点,A1、A2和B1、B2是“果圆”与x,y轴的交点,若△FF1F2是边长为1的等边三角,则a,b的值分别为( )
合成的曲线称作“果圆”(其中a2=b2+c2,a>b>c>0).如图,设点F,F1,F2是相应椭圆的焦点,A1、A2和B1、B2是“果圆”与x,y轴的交点,若△FF1F2是边长为1的等边三角,则a,b的值分别为( )


 与半椭圆
与半椭圆 合成的曲线称作“果圆”(其中a2=b2+c2,a>b>c>0).如图,设点F,F1,F2是相应椭圆的焦点,A1、A2和B1、B2是“果圆”与x,y轴的交点,若△FF1F2是边长为1的等边三角,则a,b的值分别为( )
合成的曲线称作“果圆”(其中a2=b2+c2,a>b>c>0).如图,设点F,F1,F2是相应椭圆的焦点,A1、A2和B1、B2是“果圆”与x,y轴的交点,若△FF1F2是边长为1的等边三角,则a,b的值分别为( )

