题目内容

已知圆O的直径为AB=2，C为圆O上任意一点，则|
AB
-2
AC
|=
2
2
．
分析：首先作出图形，由图可知，
AB
=
AC
+
CB
，且
AC
⊥
CB
，把待求模的向量转化为向量
AC
和
CB
，
然后求|
AB
-2
AC
|的平方，求完后开方即可．
解答：解：如图，由题意可知
CB
⊥
AC
，所以
CB
•
AC
=0，
AB
-2
AC
=
AC
+
CB
-2
AC
=
CB
-
AC
，
所以|
AB
-2
AC
|2=|
CB
-
AC
|2=(
CB
-
AC
)2=|
CB
|2-2
CB
•
AC
+|
AC
|2=|
AB
|2=4．
所以|
AB
-2
AC
|=2．
故答案为 2．
点评：本题考查了向量的模，考查了数学转化思想，解答此题的关键是运用了|
a
|2=
a
2，此题为中档题．
练习册系列答案
相关题目
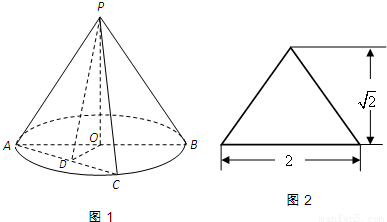
圆锥PO如图1所示，图2是它的正（主）视图．已知圆O的直径为AB，C是圆周上异于A、B的一点，D为AC的中点．
（Ⅰ） 求该圆锥的侧面积S；
（Ⅱ） 求证：平面PAC⊥平面POD；
（Ⅲ） 若∠CAB=60°，求三棱锥A-PBC的体积．

圆锥PO如图1所示，图2是它的正（主）视图．已知圆O的直径为AB，C是圆周上异于A、B的一点，D为AC的中点．

（Ⅰ） 求该圆锥的侧面积S；

（Ⅱ） 求证：平面PAC⊥平面POD；

（Ⅲ） 若∠CAB=60°，求三棱锥A﹣PBC的体积．
圆锥PO如图1所示，图2是它的正（主）视图．已知圆O的直径为AB，C是圆周上异于A、B的一点，D为AC的中点．
（Ⅰ） 求该圆锥的侧面积S；
（Ⅱ） 求证：平面PAC⊥平面POD；
（Ⅲ） 若∠CAB=60°，求三棱锥A-PBC的体积．
已知圆O的直径为AB=2，C为圆O上任意一点，则=    ．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网