题目内容
5.已知a,b,c分别是锐角△ABC的三个内角A,B,C的对边,且$\frac{2b-c}{a}$=$\frac{cosC}{cosA}$.(1)求A的大小;
(2)当$a=\sqrt{3}$时,求b+c的取值范围.
分析 (1)由正弦定理,三角函数恒等变换的应用化简已知等式可得2sinBcosA=sinB,结合sinB≠0,可求$cosA=\frac{1}{2}$,由特殊角的三角函数值即可得解A的值.
(2)由正弦定理得b=2sinB,c=2sinC,利用三角函数恒等变换的应用化简可得b+c=2$\sqrt{3}$sin(B+$\frac{π}{6}$),由$\left\{{\begin{array}{l}{A=\frac{π}{3}}\\{0<B<\frac{π}{2}}\\{\frac{π}{2}<A+B<π}\end{array}}\right.$,可求B的范围,进而可求$\frac{π}{6}$+B的范围,利用正弦函数的图象和性质即可得解其取值范围.
解答 解:(1)由正弦定理,得$\frac{2b-c}{a}=\frac{cosC}{cosA}?\frac{2sinB-sinC}{sinA}=\frac{cosC}{cosA}$,
即2sinBcosA-sinCcosA=cosCsinA,
即2sinBcosA=sinCcosA+cosCsinA=sin(A+C)=sin(π-B)=sinB,
∵sinB≠0,
∴$cosA=\frac{1}{2}$,
∵A∈(0,π),
∴$A=\frac{π}{3}$.
(2)由(1)知$A=\frac{π}{3},又a=\sqrt{3}$,由正弦定理得:$\frac{b}{sinB}=\frac{c}{sinC}=\frac{a}{sinA}=\frac{{\sqrt{3}}}{{sin\frac{π}{3}}}=2$.
∴b=2sinB,c=2sinC,
$\begin{array}{l}∴b+c=2sinB+2sinC=2sinB+2sin(A+B)=2sinB+2sinAcosB+2cosAsinB\\=2sinB+\sqrt{3}cosB+sinB=3sinB+\sqrt{3}cosB=2\sqrt{3}sin(B+\frac{π}{6})\end{array}$
∵$\left\{{\begin{array}{l}{A=\frac{π}{3}}\\{0<B<\frac{π}{2}}\\{\frac{π}{2}<A+B<π}\end{array}}\right.$,
∴$\frac{π}{6}$<B<$\frac{π}{2}$,
∴$\frac{π}{3}$<$\frac{π}{6}$+B<$\frac{2π}{3}$,
∴$\frac{\sqrt{3}}{2}$<sin(B+$\frac{π}{6}$)≤1,
∴$3<b+c≤2\sqrt{3}$.
点评 本题主要考查了正弦定理,特殊角的三角函数值,三角函数恒等变换的应用,正弦函数的图象和性质在解三角形中的应用,考查了数形结合思想,属于中档题.

 名师点拨卷系列答案
名师点拨卷系列答案| A. | $[{\frac{1}{2},\frac{5}{4}}]$ | B. | $[{0,\frac{5}{4}}]$ | C. | $({0,\frac{1}{2}}]$ | D. | (0,2] |
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
| A. | $-\frac{7}{9}$ | B. | $\frac{7}{9}$ | C. | $-\frac{1}{3}$ | D. | $\frac{1}{3}$ |
| A. | (-∞,2) | B. | (1,2) | C. | (1,+∞) | D. | (1,2)∪(2,+∞) |
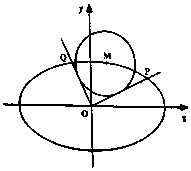 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,过点(0,-b),(a,0)的直线与原点的距离为$\sqrt{2}$,M(x0,y0)是椭圆上任一点,从原点O向圆M:(x-x0)2+(y-y0)2=2作两条切线,分别交椭圆于点P,Q.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,过点(0,-b),(a,0)的直线与原点的距离为$\sqrt{2}$,M(x0,y0)是椭圆上任一点,从原点O向圆M:(x-x0)2+(y-y0)2=2作两条切线,分别交椭圆于点P,Q.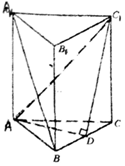 正三棱柱ABC-A1B1C1,BC=BB1=1,D为BC上一点,且满足AD⊥C1D.
正三棱柱ABC-A1B1C1,BC=BB1=1,D为BC上一点,且满足AD⊥C1D.