题目内容
我们知道,等差数列和等比数列有许多性质可以类比,现在给出一个命题:若数列{an}、{bn}是两个等差数列,它们的前n项的和分别是Sn,Tn,则
=
(1)请你证明上述命题;
(2)请你就数列{an}、{bn}是两个各项均为正的等比数列,类比上述结论,提出正确的猜想,并加以证明.
| an |
| bn |
| S2n-1 |
| T2n-1 |
(1)请你证明上述命题;
(2)请你就数列{an}、{bn}是两个各项均为正的等比数列,类比上述结论,提出正确的猜想,并加以证明.
(1)证明:
(2)猜想:数列{an}、{bn}是两个各项均为正的等比数列,它们的前n项的积分别是
|
(2)猜想:数列{an}、{bn}是两个各项均为正的等比数列,它们的前n项的积分别是
|

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
类比是一个伟大的引路人.我们知道,等差数列和等比数列有许多相似的性质,请阅读下表并根据等差数列的结论,类似的得出等比数列的两个结论:
bn= ,dn=
bn=
| 等差数列{an} | 等比数列{bn} | ||
| an=a1+(n-1)d | bn=b1qn-1 | ||
| an=am+(n-m)d | bn | ||
若cn=
则数列{cn}为等差数列 |
若dn= 则数列{dn}为等比数列 |
类比是一个伟大的引路人.我们知道,等差数列和等比数列有许多相似的性质,请阅读下表并根据等差数列的结论,类似的得出等比数列的两个结论:
bn= ,dn=
bn= ,dn=
| 等差数列{an} | 等比数列{bn} |
| an=a1+(n-1)d | bn=b1qn-1 |
| an=am+(n-m)d | bn |
若cn=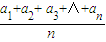 , ,则数列{cn}为等差数列 | 若dn= , 则数列{dn}为等比数列 |
