题目内容
已知函数 当
当 时,求曲线
时,求曲线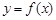 在点
在点 处的切线方程;求函数
处的切线方程;求函数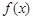 的极值
的极值
【答案】
当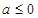 时,函数
时,函数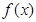 无极值
无极值
当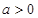 时,函数
时,函数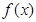 在
在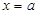 处取得极小值
处取得极小值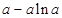 ,无极大值
,无极大值
【解析】函数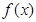 的定义域为
的定义域为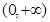 ,
,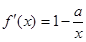 .
.
(Ⅰ)当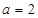 时,
时,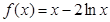 ,
,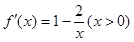 ,
,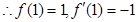 ,
,
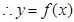 在点
在点 处的切线方程为
处的切线方程为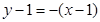 ,即
,即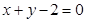 .
.
(Ⅱ)由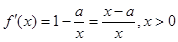 可知:
可知:
①当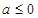 时,
时,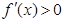 ,函数
,函数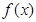 为
为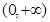 上的增函数,函数
上的增函数,函数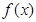 无极值;
无极值;
②当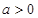 时,由
时,由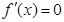 ,解得
,解得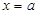 ;
;
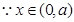 时,
时,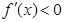 ,
,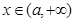 时,
时,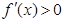
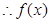 在
在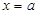 处取得极小值,且极小值为
处取得极小值,且极小值为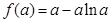 ,无极大值.
,无极大值.
综上:当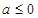 时,函数
时,函数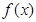 无极值
无极值
当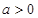 时,函数
时,函数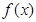 在
在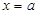 处取得极小值
处取得极小值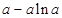 ,无极大值.
,无极大值.
此题考查的是最基本的函数切线问题及对极值含参情况的讨论,所以导数公式必需牢记,对于参数的讨论找到一个合理的分类标准做到不重不漏即可,可这往往又是学生最容易出现问题的地方。
【考点定位】 本题主要考查函数与导数、不等式的基础。注意对参数的分类讨论,属于函数中的简单题。

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
相关题目
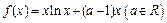 .
. 时,求曲线
时,求曲线 在
在 处的切线方程;
处的切线方程;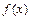 在区间
在区间 上的最小值;
上的最小值;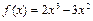 在区间
在区间 内有两个不相等的实数根,求实数a的取值范围.
内有两个不相等的实数根,求实数a的取值范围.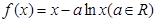
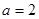 时,求曲线
时,求曲线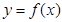 在点
在点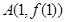 处的切线方程;
处的切线方程;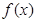 的极值.
的极值.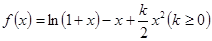
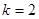 时,求曲线
时,求曲线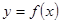 在点
在点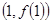 处的切线方程。
处的切线方程。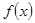 的单调区间
的单调区间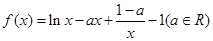 .
.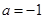 时,求曲线
时,求曲线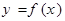 在点
在点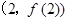 处的切线方程;
处的切线方程;
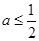 时,讨论
时,讨论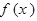 的单调性.
的单调性.