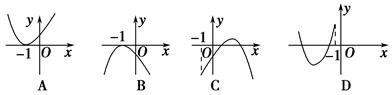
题目内容
已知定义在（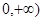
上的非负可导函数f（x）满足xf′（x）
，对任意正数
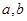，若满足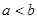
，则必有（ ）
A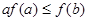． | B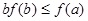． | C． | D． |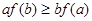
C
解析试题分析：解：因为
，所以
则函数
在区间
上为减函数
又
，所以，
所以，
故选C.
考点：1、导数的运算法则；2、导数在研究函数性质中的应用.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
若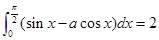
，则实数
等于（ ）
A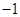． | B．1 | C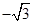． | D． |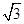
由曲线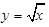
，直线
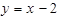及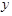
轴所围成的封闭图形的面积为( )
A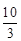． | B．4 | C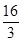． | D．6 |
下列曲线的所有切线构成的集合中,存在无数对互相垂直的切线的曲线是( )
| A．f(x)=ex | B．f(x)=x3 |
| C．f(x)=lnx | D．f(x)=sinx |
f (x)=ax3+3x2+2,若f′(-1)=4,则a的值等于( )
A． | B． | C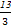． | D． |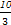
直线y＝
x＋b与曲线y＝－x＋ln x相切，则b的值为( )
| A．－2 | B．1 | C．－ | D．－1 |
已知函数f(x)＝ax－x3，对区间(0，1)上的任意x1，x2，且x1<x2，都有f(x2)－f(x1)>x2－x1成立，则实数a的取值范围为( )
| A．(0，1) | B．[4，＋∞) | C．(0，4] | D．(1，4] |
函数f(x)＝2lnx＋x2－bx＋a(b>0，a∈R)在点(b，f(b))处的切线斜率的最小值是( )
A．2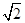 | B．2 | C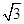． | D．1 |