题目内容
已知椭圆C的左、右焦点坐标分别是(-| 2 |
| 2 |
| ||
| 3 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)若圆P与x轴相切,求圆心P的坐标;
(Ⅲ)设Q(x,y)是圆P上的动点,当T变化时,求y的最大值.
分析:(Ⅰ)先根据离心率和焦半径求得a,进而根据a,b和c的关系求得c,则椭圆方程可得.
(Ⅱ)根据题意可知P的坐标,根据圆P与x轴相切求得x,则圆的半径的表达式可得,进而求得t,则点P的坐标可得.
(Ⅲ)由(2)知圆P的方程,把点Q代入圆的方程,求得y和t的关系,设t=cosθ,利用两角和公式化简整理根据正弦函数的性质求得y的最大值.
(Ⅱ)根据题意可知P的坐标,根据圆P与x轴相切求得x,则圆的半径的表达式可得,进而求得t,则点P的坐标可得.
(Ⅲ)由(2)知圆P的方程,把点Q代入圆的方程,求得y和t的关系,设t=cosθ,利用两角和公式化简整理根据正弦函数的性质求得y的最大值.
解答:解:(Ⅰ)因为
=
,且c=
,所以a=
,b=
=1
所以椭圆C的方程为
+y2=1
(Ⅱ)由题意知p(0,t)(-1<t<1)
由
得x=±
所以圆P的半径为
,
则有t2=3(1-t2),
解得t=±
所以点P的坐标是(0,±
)
(Ⅲ)由(Ⅱ)知,圆P的方程x2+(y-t)2=3(1-t2).因为点Q(x,y)在圆P上.所以y=t±
≤t+
设t=cosθ,θ∈(0,π),则t+
=cosθ+
sinθ=2sin(θ+
)
当θ=
,即t=
,且x=0,y取最大值2.
| c |
| a |
| ||
| 3 |
| 2 |
| 3 |
| a2-c2 |
所以椭圆C的方程为
| x2 |
| 3 |
(Ⅱ)由题意知p(0,t)(-1<t<1)
由
|
| 3(1-t2) |
所以圆P的半径为
| 3(1-t2) |
则有t2=3(1-t2),
解得t=±
| ||
| 2 |
| ||
| 2 |
(Ⅲ)由(Ⅱ)知,圆P的方程x2+(y-t)2=3(1-t2).因为点Q(x,y)在圆P上.所以y=t±
| 3(1-t2)-x2 |
| 3(1-t2) |
设t=cosθ,θ∈(0,π),则t+
| 3(1-t2) |
| 3 |
| π |
| 6 |
当θ=
| π |
| 3 |
| 1 |
| 2 |
点评:本题主要考查了直线与圆锥曲线的综合问题.考查了学生综合分析问题和解决问题的能力.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
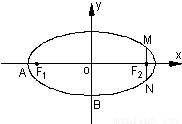
 如图,在直角坐标系xOy中,已知椭圆C:
如图,在直角坐标系xOy中,已知椭圆C:
 +
+ =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的
,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的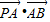 =m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.
=m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.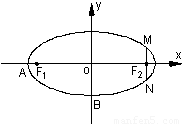
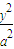 +
+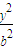 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=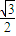 ,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的
,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的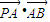 =m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.
=m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.