题目内容
已知lg2=a，lg3=b，用a，b表示log65=分析：利用换底公式将log65用lg2与lg3表示出来，再换成用字母a，b表示即可得．
解答：解：log65=
=
=
，
又由已知lg2=a，lg3=b，
故log65=
，
故答案为
| lg5 |
| lg6 |
lg
| ||
| lg2+lg3 |
| 1-lg2 |
| lg2+lg3 |
又由已知lg2=a，lg3=b，
故log65=
| 1-a |
| a+b |
故答案为
| 1-a |
| a+b |
点评：本题的考点是对数的运算性质，考查用对数的运算法则把未知的对数式用已知的对数式表示出的能力，求解此类题要细心观察变形转化的方向，避免盲目变形增加运算量．
练习册系列答案
开心练习课课练与单元检测系列答案
相关题目
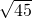的值为________．
的值为 ________．
；
的值为 ．