题目内容
已知光线经过点M(2,3),在直线l:x+y+1=0上反射,且反射光线经过点N(1,1),求
(1)入射光线与直线l的交点
(2)入射光线与反射光线所在直线的方程.
(1)入射光线与直线l的交点
(2)入射光线与反射光线所在直线的方程.
考点:与直线关于点、直线对称的直线方程
专题:计算题,直线与圆
分析:求得点M关于直线x+y+1=0的对称点M'的坐标,可得直线M'N的方程,即为反射光线所在的直线方程.求得直线M'N与直线x+y+1=0的交点C的坐标,再求得入射光线所在的直线MC的方程.
解答:
解:设点M(2,3)关于直线l:x+y+1=0的对称点M'(m,n),
则有
=1,且
+
+1=0,解得m=-4,n=-3,
即有M'(-4,-3),
则反射光线所在的直线M'N的方程为y-1=
(x-1),即为4x-5y+1=0.
由
求得直线M'N与直线x+y+1=0的交点C(-
,-
),
则入射光线所在的直线MC的方程为y-3=
(x-2),即为5x-4y+2=0,
综上,(1)入射光线与直线l的交点为C(-
,-
);
(2)入射光线所在直线方程为5x-4y+2=0,反射光线所在直线方程为4x-5y+1=0.
则有
| n-3 |
| m-2 |
| m+2 |
| 2 |
| n+3 |
| 2 |
即有M'(-4,-3),
则反射光线所在的直线M'N的方程为y-1=
| 4 |
| 5 |
由
|
| 2 |
| 3 |
| 1 |
| 3 |
则入射光线所在的直线MC的方程为y-3=
| 5 |
| 4 |
综上,(1)入射光线与直线l的交点为C(-
| 2 |
| 3 |
| 1 |
| 3 |
(2)入射光线所在直线方程为5x-4y+2=0,反射光线所在直线方程为4x-5y+1=0.
点评:本题主要考查求一个点关于直线的对称点的坐标,考查直线的方程的求法,属于中档题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
设x,y∈R,则“x+y>2”是“x,y中至少有一个数大于1”成立的.
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
设集合A={x|ln(1-x)>0},B={x|-1≤x≤1},则A∩B=( )
| A、[-1,0] |
| B、(-1,0) |
| C、[-1,0) |
| D、(-1,1) |
函数y=
的大致图象只能是( )
| 1 |
| x+2 |
A、 |
B、 |
C、 |
D、 |
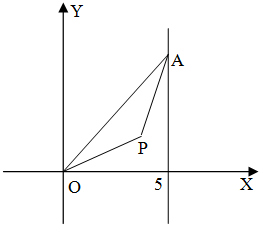 如图,点A在直线x=5上移动,等腰△OPA的顶角∠OPA为120°(O,P,A按逆时针方向排列),求点P的轨迹方程.
如图,点A在直线x=5上移动,等腰△OPA的顶角∠OPA为120°(O,P,A按逆时针方向排列),求点P的轨迹方程.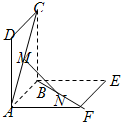 如图,已知四边形ABCD,ABEF都是矩形,M、N分别是对角线AC和BF的中点,则MN与平面BCE的关系是
如图,已知四边形ABCD,ABEF都是矩形,M、N分别是对角线AC和BF的中点,则MN与平面BCE的关系是