Question

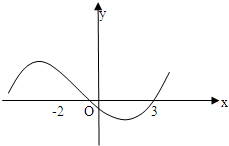知函数f（x）=ax³+bx²+cx+d（a＞0）图象如图，则y=ax2+

2

3

bx+

c

3

的单调增区间

 

．

Answer 1

分析：由已知中函数f（x）=ax³+bx²+cx+d（a＞0）图象在x=-2，x=3时取极值，故我们可以求出f′（x）的对称轴，进而分析出函数y=ax2+

2

3

bx+

c

3

的图象和性质，进而得到函数y=ax2+

2

3

bx+

c

3

的单调递增区间．

解答：解：由已知中f（x）=ax³+bx²+cx+d（a＞0）图象
∴f′（x）=3ax²+2bx+c（a＞0）的对称轴x=

-2+3

2

=

1

2

则y=ax2+

2

3

bx+

c

3

的图象是开口朝上，且以x=

1

2

为对称轴的抛物线
则y=ax2+

2

3

bx+

c

3

的单调增区间为[

1

2

，+∞)
故答案为：[

1

2

，+∞)

点评：本题考查的知识点是函数的单调性及单调区间，函数的图象与图象变化，其中根据已知条件，分析出参数a，b的关系，进而分析出函数y=ax2+

2

3

bx+

c

3

的图象和性质，是解答本题的关键．