题目内容
设z是虚数,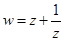 是实数,且
是实数,且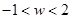 .
.
(1)求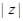 的值及z的实部的取值范围.
的值及z的实部的取值范围.
(2)设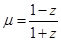 ,求
,求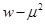 的最小值.
的最小值.
(1) ,
, 的实部的取值范围是
的实部的取值范围是 ;(2)1.
;(2)1.
解析试题分析:(1)设 且
且 ,则
,则 ,由题意
,由题意 是实数,故其虚部为0,即而
是实数,故其虚部为0,即而 ,又由
,又由 是虚数,可得
是虚数,可得 ,从而可得
,从而可得 ,即
,即 ,此时
,此时 ,由
,由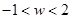 ,可得
,可得 ;
;
由(1) 得:
得:
 ,
,
因此 ,将
,将 代入,可将原式化为:
代入,可将原式化为:
 ,故可以用基本不等式求其最小值.
,故可以用基本不等式求其最小值.
(1)设 且
且 ,则
,则
∵ 是实数,∴
是实数,∴ ,又
,又 是虚数,∴
是虚数,∴ ,∴
,∴ ,即
,即 ,∴
,∴ ,
,
∵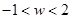 ,∴
,∴ ,即
,即 ,故z的实部取值范围
,故z的实部取值范围 ;
;
∵ ,
,
∵ ,∴
,∴ ,
,
 ,
, ,∴当
,∴当 即
即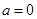 时,
时,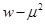 的最小值为1.
的最小值为1.
考点:1.复数的计算;2.基本不等式求最值.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
 是虚数单位.已知
是虚数单位.已知 ,则复数z对应的点落在第 ▲ 象限.
,则复数z对应的点落在第 ▲ 象限.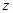 是复数,
是复数,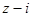 和
和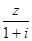 均为实数.
均为实数.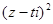 在复平面内对应点在第一象限,求实数t的取值范围.
在复平面内对应点在第一象限,求实数t的取值范围. 是(1)实数;(2)纯虚数.
是(1)实数;(2)纯虚数.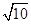 .
. ,则当m为何实数时,复数z是
,则当m为何实数时,复数z是 是实系数方程
是实系数方程 的一个虚根,且
的一个虚根,且 ,则
,则 .
.