题目内容
数列{an}满足a1=2,an+1=an2+6an+6(n∈N×)(Ⅰ)设Cn=log5(an+3),求证{Cn}是等比数列;
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)设
 ,数列{bn}的前n项的和为Tn,求证:
,数列{bn}的前n项的和为Tn,求证: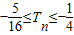 .
.
【答案】分析:(I)由已知可得,an+1+3=(an+3)2,利用构造法令Cn=log5(an+3),则可得 ,从而可证数列{cn}为等比数列
,从而可证数列{cn}为等比数列
(II)由(I)可先求数列cn,代入cn=log5(an+3)可求an
(III)把(II)中的结果代入整理可得, ,则代入Tn=b1+b2+…+bn相消可证
,则代入Tn=b1+b2+…+bn相消可证
解答:解:(Ⅰ)由an+1=an2+6an+6得an+1+3=(an+3)2,
∴ =2
=2 ,即cn+1=2cn
,即cn+1=2cn
∴{cn}是以2为公比的等比数列.
(Ⅱ)又c1=log55=1,
∴cn=2n-1,即 =2n-1,
=2n-1,
∴an+3=
故an= -3
-3
(Ⅲ)∵bn= -
- =
= -
- ,∴Tn=
,∴Tn= -
- =-
=- -
- .
.
又0<
 =
= .
.
∴- ≤Tn<-
≤Tn<-
点评:本题考查了利用定义证明等比数列:数列{an}为等比数列? ;利用构造法求数列的通项公式及数列的求和公式,属于对基本知识的综合考查.试题难度不大.
;利用构造法求数列的通项公式及数列的求和公式,属于对基本知识的综合考查.试题难度不大.
 ,从而可证数列{cn}为等比数列
,从而可证数列{cn}为等比数列(II)由(I)可先求数列cn,代入cn=log5(an+3)可求an
(III)把(II)中的结果代入整理可得,
 ,则代入Tn=b1+b2+…+bn相消可证
,则代入Tn=b1+b2+…+bn相消可证解答:解:(Ⅰ)由an+1=an2+6an+6得an+1+3=(an+3)2,
∴
 =2
=2 ,即cn+1=2cn
,即cn+1=2cn∴{cn}是以2为公比的等比数列.
(Ⅱ)又c1=log55=1,
∴cn=2n-1,即
 =2n-1,
=2n-1,∴an+3=

故an=
 -3
-3(Ⅲ)∵bn=
 -
- =
= -
- ,∴Tn=
,∴Tn= -
- =-
=- -
- .
.又0<

 =
= .
.∴-
 ≤Tn<-
≤Tn<-
点评:本题考查了利用定义证明等比数列:数列{an}为等比数列?
 ;利用构造法求数列的通项公式及数列的求和公式,属于对基本知识的综合考查.试题难度不大.
;利用构造法求数列的通项公式及数列的求和公式,属于对基本知识的综合考查.试题难度不大. 
练习册系列答案
相关题目