题目内容
估计定积分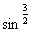
的值.
思路分析:首先计算出被积函数在给定区间上的最大值和最小值,然后利用估值定理求解.
解:∵当x∈［0,π］时,0≤sinx≤1,∴0≤x≤1,
因此有2≤2+
x≤3,
≤
≤
,
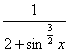于是由估值定理有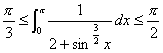
.
练习册系列答案
七星图书口算速算天天练系列答案
初中学业考试导与练系列答案
相关题目
（本小题满分14分）
Monte-Carlo方法在解决数学问题中有广泛的应用。下面是利用Monte-Carlo方法来计算定积分。考虑定积分
，这时等于由曲线
，
轴，
所围成的区域M的面积，为求它的值，我们在M外作一个边长为1正方形OABC。设想在正方形OABC内随机投掷
个点，若个点中有
个点落入
中，则的面积的估计值为
，此即为定积分的估计值I。向正方形
中随机投掷10000个点，有
个点落入区域M
(1)若=2099，计算I的值，并以实际值比较误差是否在5%以内
(2)求的数学期望
(3)用以上方法求定积分，求I与实际值之差在区间（—0.01,0.01）的概率
附表：
| n | 1899 | 1900 | 1901 | 2099 | 2100 | 2101 |
| P(n) | 0.0058 | 0.0062 | 0.0067 | 0.9933 | 0.9938 | 0.9942 |
f（x）dx≤M（b-a）由上述估值定理，估计定积分
的取值范围是 ．
f（x）dx≤M（b-a）由上述估值定理，估计定积分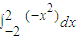
的取值范围是 ．