题目内容
【题目】在平面直角坐标系xOy中,已知向量![]() ,设
,设![]() ,向量
,向量![]() .
.
(1)若![]() ,求向量
,求向量![]() 与
与![]() 的夹角;
的夹角;
(2)若![]() 对任意实数
对任意实数![]() 都成立,求实数
都成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)向量![]() 与
与![]() 的夹角为
的夹角为![]() ;(2)
;(2)![]() 。
。
【解析】试题分析:
(1)由题意结合平面向量的坐标表示,结合平面向量的数量积运算法则可得![]() . 则向量
. 则向量![]() 与
与![]() 的夹角为
的夹角为![]() .
.
(2)原问题等价于![]() 任意实数
任意实数![]() 都成立.分离参数可得
都成立.分离参数可得![]() 任意实数
任意实数![]() 都成立.结合三角函数的性质求解关于实数
都成立.结合三角函数的性质求解关于实数![]() 的不等式可得
的不等式可得![]() .
.
试题解析:
(1)由题意, ![]() ,
, ![]() ,
,
所以 ![]() ,
, ![]() ,
,
设向量![]() 与
与![]() 的夹角为
的夹角为![]() ,
,
所以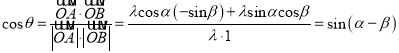 .
.
因为![]() ,即
,即![]() ,所以
,所以![]() .
.
又因为![]() ,所以
,所以![]() ,即向量
,即向量![]() 与
与![]() 的夹角为
的夹角为![]() .
.
(2)因为![]() 对任意实数
对任意实数![]() 都成立,而
都成立,而![]() ,
,
所以![]() ,即
,即![]() 任意实数
任意实数![]() 都成立. .
都成立. .
因为![]() ,所以
,所以![]() 任意实数
任意实数![]() 都成立.
都成立.
所以![]() 任意实数
任意实数![]() 都成立.
都成立.
因为![]() ,所以
,所以![]() 任意实数
任意实数![]() 都成立.
都成立.
所以![]() ,即
,即![]() ,
,
又因为![]() ,所以
,所以![]()

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目


