题目内容
已知F是
+
=1的右焦点,P是其上一点,定点B(2,1),则|PB|+
|PF|的最小值是 .
| x2 |
| 25 |
| y2 |
| 9 |
| 5 |
| 4 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:首先根据椭圆的第二定义,求出
=e=
,进一步根据准线方程求出,当BP⊥准线时|PB|+
|PF|取得最小值.
| |PF| |
| d |
| 4 |
| 5 |
| 5 |
| 4 |
解答:
 解:已知F是
解:已知F是
+
=1的右焦点,P是其上一点,
利用椭圆的第二定义:
=e=
|PF|=
d
椭圆的右准线方程:x=
则:|PB|+
|PF|的最小值为:
-2=
故答案为:
 解:已知F是
解:已知F是| x2 |
| 25 |
| y2 |
| 9 |
利用椭圆的第二定义:
| |PF| |
| d |
| 4 |
| 5 |
|PF|=
| 4 |
| 5 |
椭圆的右准线方程:x=
| 25 |
| 4 |
则:|PB|+
| 5 |
| 4 |
| 25 |
| 4 |
| 17 |
| 4 |
故答案为:
| 17 |
| 4 |
点评:本题考查的知识要点:椭圆的准线方程,椭圆的第二定义,及相关的运算问题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
在公比为整数的等比数列{an}中,若,a1+a3=6,a2+a4=12,则a3等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
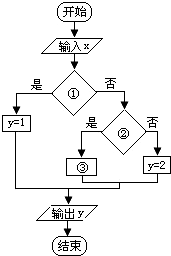 任给x的值,计算函数y=
任给x的值,计算函数y=
|
| A、x<1、x>1、y=3 |
| B、x=1、x>1、y=3 |
| C、x<1、x=1、y=3 |
| D、x<1、x>1、y=3 |
已知△ABC中,sinA:sinB:sinC=1:1:
,则此三角形的最大内角的度数是( )
| 3 |
| A、60° | B、90° |
| C、120° | D、135° |
在等差数列{an}中,已知前三项和为15,最后三项和为78,所有项和为155,则项数n=( )
| A、8 | B、9 | C、10 | D、11 |

