题目内容
已知数列{an}满足: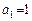 ,
,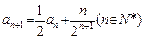 .
.
⑴求数列{an}的通项公式; ⑵证明: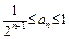
⑶设 ,且
,且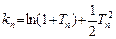 ,证明:
,证明: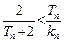 .
.
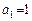 ,
,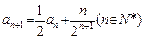 .
.⑴求数列{an}的通项公式; ⑵证明:
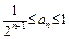
⑶设
 ,且
,且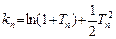 ,证明:
,证明: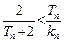 .
.(1)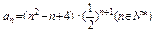 (2)(3)见解析
(2)(3)见解析
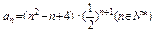 (2)(3)见解析
(2)(3)见解析:⑴由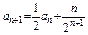 ,得
,得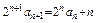 令
令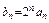 ,有
,有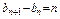
∴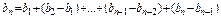 =
=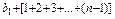 =
=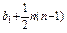
又b1=2a1=2,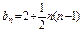
∴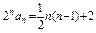 ∴
∴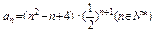
⑵证法1:(数学归纳法)
1°,当n=1时,a1=1,满足不等式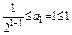
2°,假设n=k(k≥1,k∈N*)时结论成立
即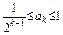 ,那么
,那么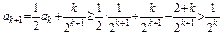
即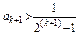 又
又
由1°,2°可知,n∈N*,都有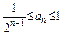 成立
成立
⑵证法2:由⑴知: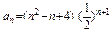 (可参照给分)
(可参照给分)
∵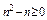 ,
,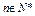 ,∴
,∴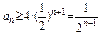
∵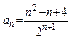 ∵
∵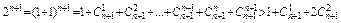
∴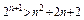 ∴
∴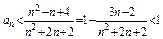 当n=1时,
当n=1时,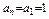 ,综上
,综上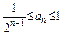
⑵证法3: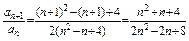
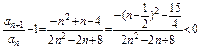
∴{an}为递减数列 当n=1时,an取最大值 ∴an≤1
由⑴中知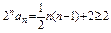
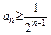
综上可知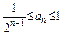
⑶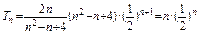 欲证:
欲证: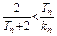 即证
即证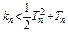
即ln(1+Tn)-Tn<0,构造函数f (x)=ln(1+x)-x
∵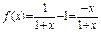 当x>0时,f ' (x)<0
当x>0时,f ' (x)<0
 ∴函数y=f (x)在(0,+∞)内递减∴f (x)在[0,+∞)内的最大值为f (0)=0
∴函数y=f (x)在(0,+∞)内递减∴f (x)在[0,+∞)内的最大值为f (0)=0
∴当x≥0时,ln(1+x)-x≤0又∵Tn>0,∴ln(1+Tn)-Tn<0∴不等式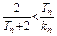 成立
成立
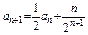 ,得
,得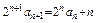 令
令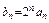 ,有
,有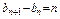
∴
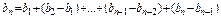 =
=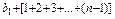 =
=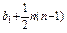
又b1=2a1=2,
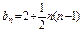
∴
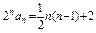 ∴
∴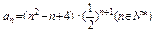
⑵证法1:(数学归纳法)
1°,当n=1时,a1=1,满足不等式
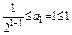
2°,假设n=k(k≥1,k∈N*)时结论成立
即
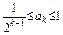 ,那么
,那么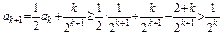
即
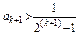 又
又
由1°,2°可知,n∈N*,都有
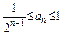 成立
成立 ⑵证法2:由⑴知:
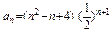 (可参照给分)
(可参照给分)∵
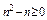 ,
,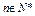 ,∴
,∴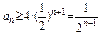
∵
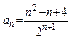 ∵
∵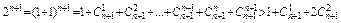
∴
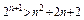 ∴
∴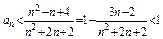 当n=1时,
当n=1时,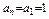 ,综上
,综上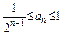
⑵证法3:
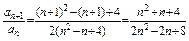
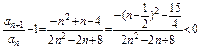
∴{an}为递减数列 当n=1时,an取最大值 ∴an≤1
由⑴中知
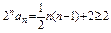
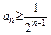
综上可知
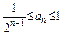
⑶
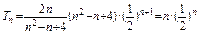 欲证:
欲证: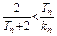 即证
即证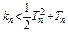
即ln(1+Tn)-Tn<0,构造函数f (x)=ln(1+x)-x
∵
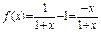 当x>0时,f ' (x)<0
当x>0时,f ' (x)<0 ∴函数y=f (x)在(0,+∞)内递减∴f (x)在[0,+∞)内的最大值为f (0)=0
∴函数y=f (x)在(0,+∞)内递减∴f (x)在[0,+∞)内的最大值为f (0)=0∴当x≥0时,ln(1+x)-x≤0又∵Tn>0,∴ln(1+Tn)-Tn<0∴不等式
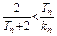 成立
成立 
练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
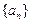 满足:
满足: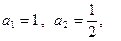 且
且 .
.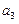 ,
,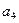 ,
,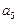 ,
,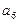 的值及数列
的值及数列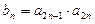 ,求数列
,求数列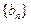 的前
的前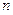 项和
项和 ;
;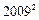
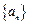 是等差数列,从
是等差数列,从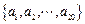 中任取3个不同的数,使这3个数仍成等差数列,则这样不同的等差数列的个数最多有( )
中任取3个不同的数,使这3个数仍成等差数列,则这样不同的等差数列的个数最多有( )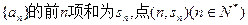 在函数
在函数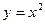 的图象上,数列
的图象上,数列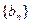 满足
满足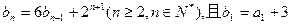 (1)求数列
(1)求数列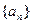 的通项公式;(2)证明列数
的通项公式;(2)证明列数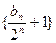 是等比数列,并求数列
是等比数列,并求数列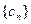 满足对任意的
满足对任意的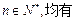
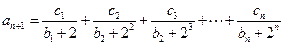 成立,
成立,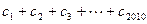 的值。
的值。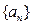 的前n项和
的前n项和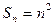 ,
, 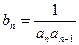 ,求数列
,求数列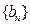 的前n项和
的前n项和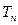 .
.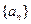
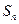
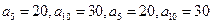
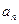 ; (2)若
; (2)若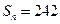 ,求n
,求n