题目内容
在△ABC中,BC=2,AC=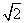 ,AB=
,AB=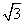 +1。
+1。
(Ⅰ)求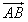 ·
·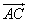 ;
;
(Ⅱ)设△ABC的外心为O,若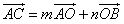 ,求m、n的值。
,求m、n的值。
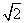 ,AB=
,AB=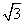 +1。
+1。(Ⅰ)求
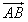 ·
·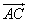 ;
;(Ⅱ)设△ABC的外心为O,若
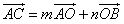 ,求m、n的值。
,求m、n的值。解:(Ⅰ)由余弦定理知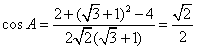 ,
,
∴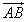 ·
·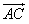 =|
=|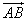 |·|
|·|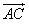 |cosA=
|cosA=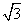 +1。
+1。
(Ⅱ)由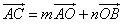 ,
,
知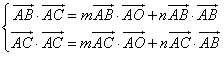 ,
,
∴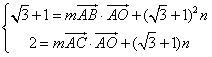 ,
,
∵O为△ABC的外心,
∴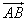 ·
·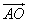 =|
=|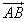 |·|
|·|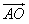 |cos∠BAO=
|cos∠BAO=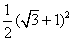 ,
,
同理,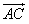 ·
·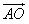 =1,
=1,
即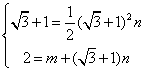 ,
,
解得:m= ,n=
,n=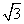 。
。
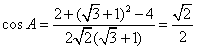 ,
,∴
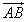 ·
·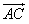 =|
=|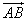 |·|
|·|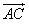 |cosA=
|cosA=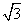 +1。
+1。 (Ⅱ)由
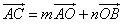 ,
,知
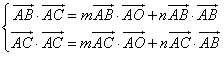 ,
,∴
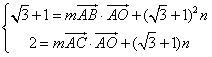 ,
,∵O为△ABC的外心,
∴
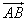 ·
·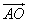 =|
=|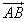 |·|
|·|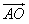 |cos∠BAO=
|cos∠BAO=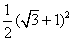 ,
,同理,
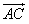 ·
·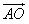 =1,
=1, 即
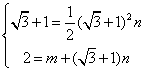 ,
,解得:m=
 ,n=
,n=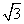 。
。
练习册系列答案
相关题目
在△ABC中,|BC|=2|AB|,∠ABC=120°,则以A,B为焦点且过点C的双曲线的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在△ABC中,(
+
)•
=|
|2,
•
=3,|
|=2,则△ABC的面积是( )
| BC |
| BA |
| AC |
| AC |
| BA |
| BC |
| BC |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |