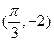题目内容
在平面直角坐标系中,角 的始边为
的始边为 轴的非负半轴,点
轴的非负半轴,点 在角
在角 的终边上,点Q
的终边上,点Q 在角
在角 的终边上,且
的终边上,且 .
.
(1)求 ;
;
(2)求P,Q的坐标,并求 的值.
的值.
 的始边为
的始边为 轴的非负半轴,点
轴的非负半轴,点 在角
在角 的终边上,点Q
的终边上,点Q 在角
在角 的终边上,且
的终边上,且 .
.(1)求
 ;
; (2)求P,Q的坐标,并求
 的值.
的值.(1) ;(2)
;(2) ,
, ,
, .
.
 ;(2)
;(2) ,
, ,
, .
.试题分析:(1)由条件中
 ,
, 可知
可知 ,
, ,再由
,再由 可得
可得 ,利用二倍角公式的降幂变形,可将其转化为关于
,利用二倍角公式的降幂变形,可将其转化为关于 的方程:
的方程: ;(2)由(1)可知
;(2)由(1)可知 ,
, ,即有
,即有 ,
, ,从而
,从而 ,
, ,根据任意角的三角函数的定义,可知
,根据任意角的三角函数的定义,可知 ,
, ,
, ,
, ,再由两角和的正弦公式即可得
,再由两角和的正弦公式即可得 .
.试题解析:(1)∵
 ,
, ,∴
,∴ ,
, ,
,又∵
 ,∴
,∴ ,即
,即 ;
;(2)由(1)可知
 ,
, ,∴
,∴ ,
, ,
,∴
 ,
, ,∴
,∴ ,
, ,
, ,
, ,
, .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
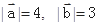 .(1)若
.(1)若 的夹角为60o,求
的夹角为60o,求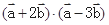 ;
;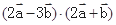 =61,求
=61,求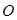 为坐标原点,
为坐标原点,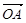 =(
=(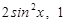 ),
),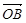 =(1,
=(1,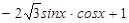 ),
), 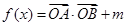 .
.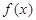 的定义域为[-
的定义域为[-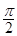 ,
,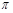 ],求y=
],求y=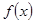 的定义域为[
的定义域为[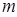 的值.
的值.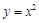 的图象F按向量
的图象F按向量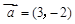 平移到
平移到 ,则
,则 点P在
点P在 轴上,且使
轴上,且使 有最小值,则点P 的坐标为
有最小值,则点P 的坐标为 存在唯一的实数
存在唯一的实数 ,使得向量
,使得向量 ;
; 为单位向量,且向量
为单位向量,且向量 ,则向量
,则向量 ;
; ;
; ,则向量
,则向量 ;
; ,则
,则 。
。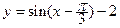 的图象经过按
的图象经过按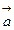 平移得到
平移得到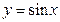 的图象,则
的图象,则