题目内容
直线x+ay=2a+2与ax+y=a+1平行(不重合)的充要条件是
- A.

- B.

- C.a=1
- D.a=-1
C
分析:直线平行(不重合)有两种情况:先判断直线有无斜率,有斜率时则斜率相等且不过相同点,无斜率时在x轴上的截距不相等.
解答:直线x+ay=2a+2与ax+y=a+1平行(不重合),易知ax+y=a+1有斜率,斜率k=-a,直线x+ay=2a+2的斜率为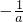 ;
;
所以-a=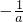 ;所以a=±1,当a=-1时直线x+ay=2a+2与ax+y=a+1重合,所以a=1
;所以a=±1,当a=-1时直线x+ay=2a+2与ax+y=a+1重合,所以a=1
故选C
点评:平行的充要条件有斜率和无斜率两种情况,不可漏掉无斜率情况;当然还可用系数之比来解.
分析:直线平行(不重合)有两种情况:先判断直线有无斜率,有斜率时则斜率相等且不过相同点,无斜率时在x轴上的截距不相等.
解答:直线x+ay=2a+2与ax+y=a+1平行(不重合),易知ax+y=a+1有斜率,斜率k=-a,直线x+ay=2a+2的斜率为
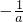 ;
;所以-a=
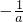 ;所以a=±1,当a=-1时直线x+ay=2a+2与ax+y=a+1重合,所以a=1
;所以a=±1,当a=-1时直线x+ay=2a+2与ax+y=a+1重合,所以a=1故选C
点评:平行的充要条件有斜率和无斜率两种情况,不可漏掉无斜率情况;当然还可用系数之比来解.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
直线x+ay=2a+2与ax+y=a+1平行(不重合)的充要条件是( )
A、a=
| ||
B、a=-
| ||
| C、a=1 | ||
| D、a=-1 |

