题目内容
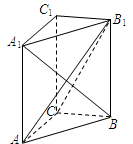
如图,在直三棱柱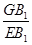 中,已知
中,已知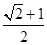 ,
,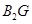 ,
,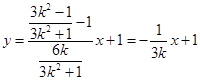 .
.
(1)求异面直线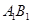 与
与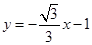 夹角的余弦值;
夹角的余弦值;
(2)求二面角 平面角的余弦值.
平面角的余弦值.
(1)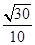 ,(2)
,(2)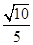 .
.
解析试题分析:(1)利用空间向量求线线角,关键在于正确表示各点的坐标. 以 为正交基底,建立空间直角坐标系
为正交基底,建立空间直角坐标系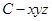 .则
.则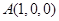 ,
, ,
,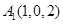 ,
,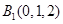 ,所以
,所以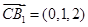 ,
,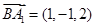 ,因此
,因此 ,所以异面直线
,所以异面直线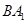 与
与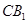 夹角的余弦值为
夹角的余弦值为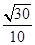 .(2)利用空间向量求二面角,关键在于求出一个法向量. 设平面
.(2)利用空间向量求二面角,关键在于求出一个法向量. 设平面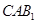 的法向量为
的法向量为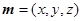 ,则
,则 即
即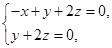 取平面
取平面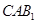 的一个法向量为
的一个法向量为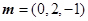 ;同理可得平面
;同理可得平面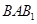 的一个法向量为
的一个法向量为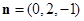 ;由两向量数量积可得二面角
;由两向量数量积可得二面角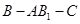 平面角的余弦值为
平面角的余弦值为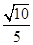 .
.
试题解析: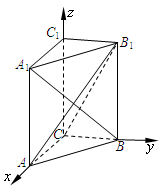
如图,以 为正交基底,建立空间直角坐标系
为正交基底,建立空间直角坐标系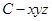 .
.
则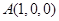 ,
, ,
,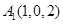 ,
,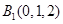 ,所以
,所以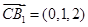 ,
,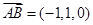 ,
,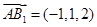 ,
,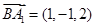 .
.
(1)因为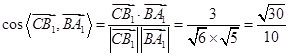 ,
,
所以异面直线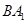 与
与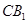 夹角的余弦值为
夹角的余弦值为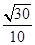 . 4分
. 4分
(2)设平面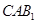 的法向量为
的法向量为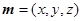 ,
,
则 即
即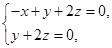
取平面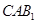 的一个法向量为
的一个法向量为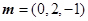 ;
;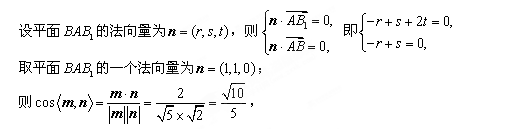
所以二面角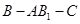 平面角的余弦值为
平面角的余弦值为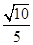 . 10分
. 10分
考点:利用空间向量求线线角及二面角

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
 的底面
的底面 是等腰直角三角形,
是等腰直角三角形, ,侧棱
,侧棱 底面
底面 ,
, 是
是 的中点,
的中点, 是
是 上的点.
上的点. 与
与 的大小(结果用反三角函数表示);
的大小(结果用反三角函数表示); ,求线段
,求线段 的长.
的长.
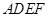 与梯形
与梯形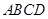 所在的平面互相垂直,
所在的平面互相垂直,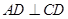 ,
, ∥
∥ ,
,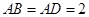 ,
,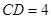 ,
,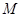 为
为 的中点.
的中点.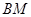 ∥平面
∥平面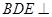 平面
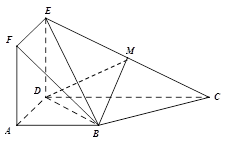
平面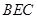 ;
;
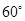 ,∠BAC
,∠BAC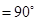 ,AD是BC上的高,沿AD把△ABD折起,使∠BDC
,AD是BC上的高,沿AD把△ABD折起,使∠BDC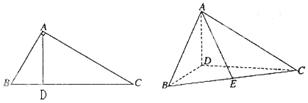
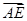 与
与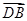 夹角的余弦值.
夹角的余弦值.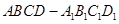 的棱长为2,E、F分别是
的棱长为2,E、F分别是 、
、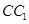 的中点,过
的中点,过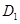 、E、F作平面
、E、F作平面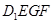 交
交 于G.
于G.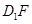 ;
;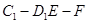 的余弦值;
的余弦值;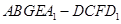 的体积.
的体积.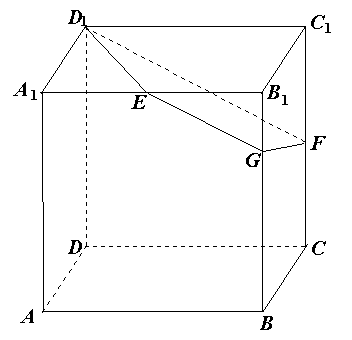
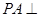 底面ABCD,
底面ABCD,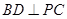 ,E是PA的中点.
,E是PA的中点.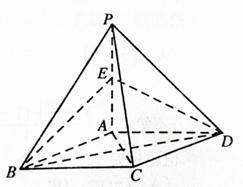
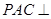 平面EBD;
平面EBD;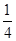 ,求四棱锥P-ABCD的体积.
,求四棱锥P-ABCD的体积. 为平行四边形,
为平行四边形,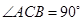 ,
,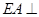 平面
平面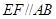 ,
,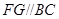 ,
,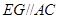 ,
,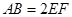 .
.
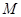 是线段
是线段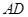 的中点,求证:
的中点,求证: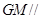 平面
平面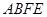 ;
;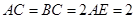 ,求二面角
,求二面角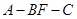 的余弦值.
的余弦值.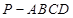 中,
中,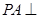 面
面 ,
,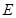 、
、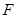 分别为
分别为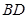 、
、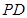 的中点,
的中点, ,
,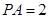 .
.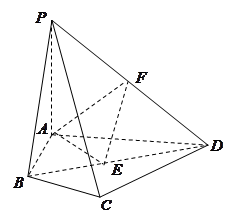
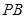 ∥面
∥面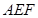 ;
;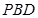 与面
与面 ,
, (
( 两两互相垂直的单位向量),那么
两两互相垂直的单位向量),那么 = .
= .