题目内容
4.已知M(a,5-a,2a-1),N(1,a+2,2-a)两点,当|MN|取得最小值时,a的值是( )| A. | 19 | B. | $\frac{19}{14}$ | C. | -$\frac{8}{7}$ | D. | $\frac{8}{7}$ |
分析 利用空间零点的距离公式以及二次函数的性质求解距离的最值即可.
解答 解:M(a,5-a,2a-1),N(1,a+2,2-a)两点,
|MN|=$\sqrt{(a-1)^{2}+(5-a-a-2)^{2}+(2a-1-2+a)^{2}}$=$\sqrt{14{a}^{2}-32a+19}$=$\sqrt{14({a-\frac{8}{7})}^{2}+\frac{5}{7}}$≥$\frac{\sqrt{35}}{7}$,当且仅当a=$\frac{8}{7}$取等号.
故选:D.
点评 本题考查空间距离公式的应用,二次函数的最值,考查计算能力.

练习册系列答案
相关题目
14.已知定义在R上的奇函数f(x)满足f(x+2)=-f(x),且f(1)=2,则f(2015)的值为( )
| A. | 2 | B. | 0 | C. | -2 | D. | -1 |
16.设a1,a2,…an是正整数1,2,3,…,n的一个排列,令bj表示排在j的左边且比j大的数的个数,称为j的逆序数.如在排列3,5,1,4,2,6中,5的逆序数是0,2的逆序数是3,则由1至8这8个数字构成的所有排列中,满足1的逆序数是2,2的逆序数是3,5的逆序数是3的不同排列种数是( )
| A. | 144 | B. | 172 | C. | 180 | D. | 192 |
13.下列说法中正确的序号为( )
| A. | 若直线l平行于平面α内的无数条直线,则l∥α; | |
| B. | 若α∥β,a?α,b?β,则a与b是异面直线; | |
| C. | 若α∥β,a?α,则a∥β; | |
| D. | 若α∩β=b,a?α,则a与β一定相交. |
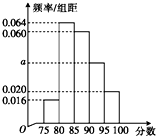 某高校在某年的自主招生考试成绩中随机抽取50名学生的笔试成绩,绘制成频率分布直方图如图所示,若要从成绩在[85,90),[90,95),[95,100]三组内的学生中,用分层抽样的方法抽取12人参加面试,则成绩在[90,100]内的学生应抽取的人数为6.
某高校在某年的自主招生考试成绩中随机抽取50名学生的笔试成绩,绘制成频率分布直方图如图所示,若要从成绩在[85,90),[90,95),[95,100]三组内的学生中,用分层抽样的方法抽取12人参加面试,则成绩在[90,100]内的学生应抽取的人数为6.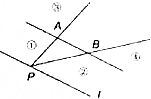 如图,点P是直线l上一点,l∥直线AB,如果存在实数x,y,使得$\overrightarrow{PC}=x\overrightarrow{PA}+y\overrightarrow{PB}$,且x+y=2,x>2,则点C所在的区域是图中标示的区域( )
如图,点P是直线l上一点,l∥直线AB,如果存在实数x,y,使得$\overrightarrow{PC}=x\overrightarrow{PA}+y\overrightarrow{PB}$,且x+y=2,x>2,则点C所在的区域是图中标示的区域( )