题目内容
定义在R上的函数f(x)既是奇函数又是以2为周期的周期函数,则f(1)等于________
解析试题分析:根据奇函数和周期函数的性质可以知道,由于定义在R上的函数f(x)是奇函数,又是以2为周期的周期函数,可得-f(1)=f(-1)=f(-1+2)=f(1),f(1)=0.
由于定义在R上的函数f(x)是奇函数,又是以2为周期的周期函数,
所以-f(1)=f(-1)=f(-1+2)=f(1),所以f(1)=0.
故答案为:0
考点:函数奇偶性的定义和周期函数

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
若 ,则
,则 ( )
( )
| A.2 | B.2或-2 | C. | D.-2 |
设 ,若
,若 是
是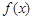 的最小值,则
的最小值,则 的取值范围为( )
的取值范围为( )
| A.[-1,2] | B.[-1,0] | C.[1,2] | D.[0,2] |
已知 ,则
,则 =( )
=( )
| A.-3 | B.1 | C.-1 | D.4 |
在映射 中,
中, ,且
,且 ,则与A中的元素
,则与A中的元素 在B中的象为( ).
在B中的象为( ).
A. | B. | C. | D. |
 与
与 有4个不同的交点,则
有4个不同的交点,则 的范围( )
的范围( )
| A.(-4,0) | B.[0,4] | C.[0,4) | D.(0,4) |
函数 为偶函数,且
为偶函数,且 上单调递减,则
上单调递减,则 的一个单调递增区间为( )
的一个单调递增区间为( )
A. | B. | C. | D. |
 的定义域为_______________________.
的定义域为_______________________. 的单调减区间是 .
的单调减区间是 .